Sólidos Geométricos - Área e Volume do Prisma
O prisma é um sólido geométrico e antes de aprendermos a calcular o seu volume vamos discorrer um pouco sobre ele.
Trata-se de um poliedro convexo que contém duas faces congruentes e paralelas formadas por um polígono convexo. Estas faces são denominadas base ou diretriz. Contém também faces laterais em igual número de lados dos polígonos da base.
A forma geométrica da base é que dá nome ao prisma, por exemplo, o prisma pentagonal é assim denominado por possuir faces diretrizes com 5 lados. Um pentágono possui cinco lados.
Os polígonos da base podem ou não ser regulares. Um polígono é dito regular quando todos os seus lados e ângulos internos são congruentes.
As bases de um prisma encontram-se em planos paralelos, assim para identificarmos quais faces são as bases de um prisma basta observarmos quais são as duas faces iguais e paralelas, normalmente sua forma geométrica também é diferente das demais faces laterais, embora possam haver faces laterais que sejam paralelas entre si, como as do prisma hexagonal regular, visto mais abaixo no exemplo de cálculo da área do prisma.
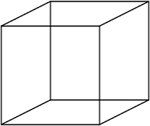
Provavelmente o prisma com o qual você esteja mais familiarizado seja o cubo, tal qual o da figura à direita e talvez você nem tenha percebido que o cubo é um prisma.
O cubo é um prisma reto já que as suas arestas laterais são perpendiculares às bases.
O cubo também é um prisma regular, pois além de ser um prisma reto, suas bases são polígonos regulares, visto que são quadrados.
Além disto, em um cubo todas as faces são congruentes.
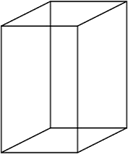
Um outro prisma com o qual você deve estar habituado é o paralelepípedo retângulo como o da figura ao lado.
Note que assim como o cubo, o paralelepípedo retângulo também é um prisma reto, visto que as suas arestas laterais igualmente são perpendiculares às bases, no entanto só será um prisma regular quando as suas bases forem quadradas. Retângulos não são polígonos regulares.
As faces laterais de um paralelepípedo retângulo são retângulos.
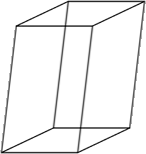
Finalizando estas poucas explicações temos ao lado a figura de um paralelepípedo oblíquo:
As faces laterais de um paralelepípedo oblíquo são paralelogramos.
Lembre-se que todo retângulo é um paralelogramo, mas nem todo paralelogramo é um retângulo.
Em resumo, todo prisma oblíquo, como o paralelepípedo ao lado, tem arestas laterais não perpendiculares às bases e as suas faces laterais são paralelogramos.
Cálculo da Área da Superfície do Prisma
A área total do prisma será a soma do valor da área das duas bases mais a área de todas as suas faces laterais.
Independentemente de um prisma ser reto ou oblíquo, a soma das áreas de todas as suas faces laterais pode ser obtida multiplicando-se o perímetro de uma das faces base pela medida da sua altura.
Exemplo de Cálculo da Área da Superfície do Prisma
A área das bases irá depender da forma do polígono. Vamos tomar como exemplo o prisma hexagonal regular visto na figura ao lado:
Vamos assumir que a altura do prisma seja igual a 100 cm e que a medida dos lados do hexágono das bases seja igual a 24 cm cada uma.
Qual é a área total deste prisma?
Como as bases são hexágonos regulares, a área de cada um deles pode ser calculada através da seguinte fórmula:
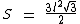, onde S é a área do hexágono regular e l a medida de cada lado do hexágono.
Como neste exemplo l = 24 temos que a área de cada face da base será:
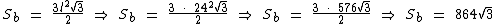
O total da área das faces laterais é igual ao perímetro da base multiplicada pela altura do prisma. Como o hexágono regular deste exemplo tem seis lados que medem 24 cm cada um, o seu perímetro será:
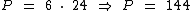
Logo o total da área das faces laterais será este perímetro multiplicado pela altura do prisma:
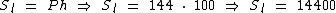
A superfície total do prisma será:
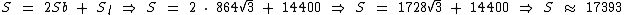
Portanto a área total do prisma hexagonal em questão é de aproximadamente 17393 cm2 ou aproximadamente 1,7393 m2.
Cálculo do Volume do Prisma
Não importa se um prisma é ou não regular, se é um prisma reto ou oblíquo, o cálculo do seu volume sempre será obtido multiplicando-se o valor da área da base pela sua altura.
Exemplo de Cálculo do Volume do Prisma
Vamos calcular o volume do paralelepípedo oblíquo ao lado:
Suponhamos que neste exemplo o paralelepípedo meça 20 cm de comprimento, 20 cm de largura e 40 cm de altura.
O seu volume é calculado através da seguinte fórmula:
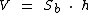
Como as bases são quadradas, podemos assim calcular a área das mesmas:
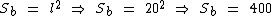
Logo o volume do paralelepípedo oblíquo será:
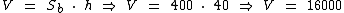
Concluindo este artigo, o volume do paralelepípedo oblíquo deste exemplo é igual a 16000 cm3 ou 0,016 m3.
Caso seja do seu interesse, temos um artigo no qual tratamos especificamente o cálculo da área de um polígono regular.
