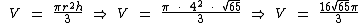Dados uma base circular contida em um plano e um ponto não situado neste plano, cone circular é um sólido geométrico composto de todos os segmentos de reta que possuem uma extremidade em qualquer ponto do círculo e a outra no ponto.
Sólidos Geométricos - Área e Volume do Cone Circular
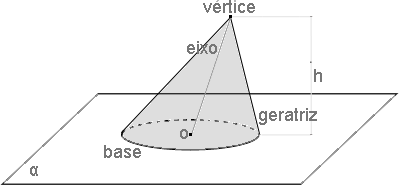
A superfície do cone circular é delimitada pelo círculo da base e pela superfície lateral formada por todas as suas geratrizes.
Uma geratriz de um cone circular é qualquer segmento de reta com uma extremidade na circunferência da base e com a outra extremidade no seu vértice.
O vértice de um cone circular é o referido ponto não coplanar ao círculo da base.
O eixo de um cone circular é o segmento de reta cujos extremos são o centro da base e o vértice do cilindro.
A altura de um cone circular é a distância entre o vértice e o círculo (plano) da base.
Cone Circular Reto ou Oblíquo
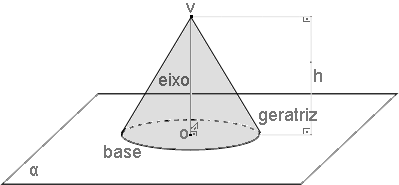
Um cone circular reto possui o seu eixo perpendicular ao plano da base e o eixo é congruente à sua altura. As geratrizes são congruentes entre si.
A projeção ortogonal do vértice no plano da base é o centro da base, ou seja, visto o cone de cima o vértice sobrepõe o centro da base.
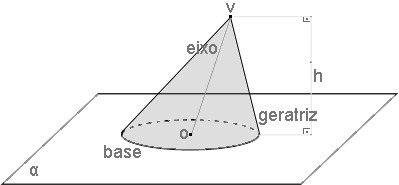
Um cone circular oblíquo possui o seu eixo oblíquo ao plano da base e o eixo não é congruente à sua altura. As geratrizes não são congruentes entre si.
A projeção ortogonal do vértice no plano da base não é o centro da base, isto é, visto o cone de cima o vértice não sobrepõe o centro da base.
Cálculo da Área da Superfície do Cone Circular Reto
A área total da superfície de um cone circular é a soma da área da superfície lateral com a área do círculo da base.
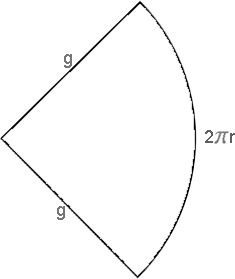
Se tivermos um cone circular reto, a sua superfície lateral poderá ser planificada quando obteremos, então, um setor circular tendo como raio a medida da geratriz (todas as geratrizes de um cone circular reto são congruentes entre si) e a medida do arco será 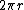 , o comprimento da circunferência da base do cone.
, o comprimento da circunferência da base do cone.
No caso do cone circular oblíquo, quando planificada a sua superfície lateral não obtemos um setor circular, visto que as geratrizes não são congruentes entre si, o que não nos permite utilizar o mesmo método para o cálculo da sua área lateral.
Quando conhecemos o raio e o comprimento do arco podemos calcular a sua área através da seguinte fórmula:
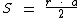
Onde r é a medida do raio e a é a medida do arco.
Como a área da superfície lateral de um cone circular reto é igual a área de um setor circular cujo raio é a medida da geratriz g e o comprimento do arco é o comprimento da circunferência da base do cone, isto é, 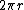 , onde r é a medida do raio da base, temos que a área da superfície lateral é dada por:
, onde r é a medida do raio da base, temos que a área da superfície lateral é dada por:
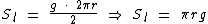
A área da base é igual ao produto de  pelo quadrado do seu raio, já que a base é um círculo:
pelo quadrado do seu raio, já que a base é um círculo:
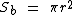
Em vez de utilizarmos duas fórmulas, uma para calcular a área da superfície lateral e uma outra para calcular a área da base circular e depois as somarmos, podemos fazer uso de apenas uma fórmula:
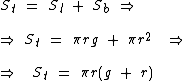
Exemplo de Cálculo da Área da Superfície do Cone Circular Reto
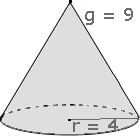
Vamos calcular a área total da superfície do cone ao lado a partir dos dados fornecidos.
Utilizaremos a fórmula vista acima:
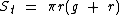
Os dados fornecidos pela figura são:
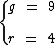
Os substituindo na fórmula obtemos a área total do cone:
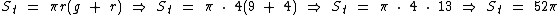
Cálculo do Volume do Cone Circular
Independentemente de um cone circular ser reto ou oblíquo, a medida do seu volume é igual a um terço do produto da área da base pela altura do cone, o qual podemos expressar através da seguinte fórmula:
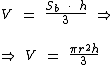
Exemplo de Cálculo do Volume do Cone Circular
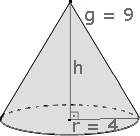
Calculemos o volume do cone circular reto visto no exemplo anterior.
Continuam sendo estes os dados fornecidos pela ilustração:
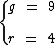
Realizaremos o cálculo do volume do cone circular através desta fórmula:
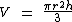
Note que a figura não nos fornece a medida da altura, no entanto conhecemos a medida da geratriz e a medida do raio da base.
Observe na gravura que g, h e r são os lados de um triângulo retângulo, assim através do Teorema de Pitágoras podemos obter a altura do cone:
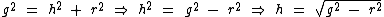
Então a partir do raio da base e da geratriz chegamos à medida da altura:
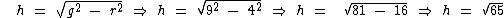
Substituindo as variáveis pelos valores na fórmula do volume do cone circular reto: