Razão
Conceitualmente a razão do número a para o número b, sendo b ≠ 0, é igual ao quociente de a por b que podemos representar das seguintes formas:
As razões acima podem ser lidas como:
- razão de a para b
- a está para b
- a para b
Em qualquer razão, ao termo a chamamos de antecedente e ao termo b chamamos de consequente.
Razão inversa ou recíproca
Vejamos as seguintes razões:
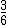
e
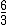
Elas são tidas como razões inversas ou recíprocas.

Note que o antecedente de uma é o consequente da outra e vice-versa.
Uma propriedade das razões inversas é que o produto delas é sempre igual a 1, isto se deve ao fato de uma ser o inverso multiplicativo da outra.
Agora vejamos as seguintes razões:
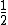
e
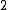
A primeira razão possui os números 1 e 2 como seu respectivo antecedente e consequente, já a segunda razão possui o número 2 como o seu antecedente e o número 1, omitido, como o seu consequente. Em função disto, pelo antecedente de uma ser o consequente da outra e vice-versa, estas duas razões também são inversas uma em relação a outra.
Apesar de uma razão ser apresentada na forma de uma fração ou de uma divisão, você pode calcular o seu valor final a fim de se obter o seu valor na forma decimal. Por exemplo:
A razão de 15 para 5 é 3, pois 15 : 5 = 3 na forma decimal, ou seja, 15 é o triplo de 5.
Neste outro caso, a razão de 3 para 4 é 0,75, pois 3 : 4 = 0,75 na forma decimal.
Razão centesimal
Como visto acima, a razão de 3 para 4 é 0,75, pois 3 : 4 = 0,75 na forma decimal, ou seja, 3 equivale a 75% de 4. 75% nada mais é que uma razão de antecedente igual 75 e consequente igual a 100. É por isto é chamada de razão centesimal.
Exemplos
 O salário de Paulo é de R$ 2.000,00 e João tem um salário de R$ 1.000,00. Qual a razão de um salário para outro?
O salário de Paulo é de R$ 2.000,00 e João tem um salário de R$ 1.000,00. Qual a razão de um salário para outro?
Temos: Salário de Paulo : Salário de João.
Então:
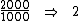
A razão acima pode ser lida como a razão de 2000 para 1000, ou 2000 está para 1000. Esta razão é igual a 2, o que equivale a dizer que o salário de Paulo é o dobro do salário de João, ou seja, através da razão estamos fazendo uma comparação de grandezas, que neste caso são os salários de Paulo e João.
 Portanto a razão de um salário para outro é igual a 2.
Portanto a razão de um salário para outro é igual a 2.
 Eu tenho uma estatura de 1,80m e meu filho tem apenas 80cm de altura. Qual é a razão de nossas alturas?
Eu tenho uma estatura de 1,80m e meu filho tem apenas 80cm de altura. Qual é a razão de nossas alturas?
Como uma das medidas está em metros e a outra em centímetros, devemos colocá-las na mesma unidade. Sabemos que 1,80m é equivalente a 180cm. Temos então a razão de 180cm para 80cm:
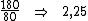
 2,25 é a razão de nossas alturas.
2,25 é a razão de nossas alturas.
