Proporção
A igualdade entre razões denomina-se proporção.
Os números a, b, c e d, todos diferentes de zero, formam nesta ordem, uma proporção se, e somente se, a razão a : b for igual à razão c : d.
Indicamos esta proporção por:
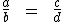
Chamamos aos termos a e d de extremos e aos termos b e c chamamos de meios.
Veja que a razão de 10 para 5 é igual a 2 (10 : 5 = 2).
A razão de 14 para 7 também é igual a 2 (14 : 7 = 2).

Podemos então afirmar que estas razões são iguais e que a igualdade abaixo representa uma proporção:
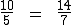
Lê-se a proporção acima da seguinte forma:
"10 está para 5, assim como 14 está para 7".
Propriedade fundamental das proporções
Qualquer que seja a proporção, o produto dos extremos é igual ao produto dos meios. Assim sendo, dados os números a, b, c e d, todos diferentes de zero e formando nesta ordem uma proporção, então o produto de a por d será igual ao produto de b por c:
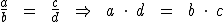
Segunda propriedade das proporções
Qualquer que seja a proporção, a soma ou a diferença dos dois primeiros termos está para o primeiro, ou para o segundo termo, assim como a soma ou a diferença dos dois últimos termos está para o terceiro, ou para o quarto termo. Então temos:
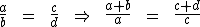 ou
ou 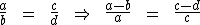
Ou
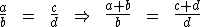 ou
ou 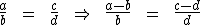
Terceira propriedade das proporções
Qualquer que seja a proporção, a soma ou a diferença dos antecedentes está para a soma ou a diferença dos consequentes, assim como cada antecedente está para o seu respectivo consequente. Temos então:
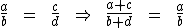 ou
ou 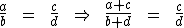
Ou
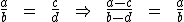 ou
ou 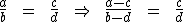
Quarta proporcional
Dados três números a, b, e c, chamamos de quarta proporcional o quarto número x que junto a eles formam a proporção:
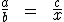
Tendo o valor dos números a, b, e c, podemos obter o valor da quarta proporcional, o número x, recorrendo à propriedade fundamental das proporções. O mesmo procedimento utilizado na resolução de problemas de regra de três simples.
Terceira proporcional
Em uma proporção onde os meios são iguais, um dos extremos é a terceira proporcional do outro extremo:
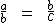
Na proporção acima a é a terceira proporcional de c e vice-versa.
Exemplos
 Paguei R$15,00 por 1kg de carne. Se eu tivesse pago R$25,00 teria comprado 2kg. A igualdade da razão do preço de compra pela quantidade, dos dois casos, resulta em uma proporção?
Paguei R$15,00 por 1kg de carne. Se eu tivesse pago R$25,00 teria comprado 2kg. A igualdade da razão do preço de compra pela quantidade, dos dois casos, resulta em uma proporção?
Os termos da nossa suposta proporção são: 15, 1, 25 e 2.
Podemos utilizar a propriedade fundamental das proporções para verificamos se tais termos nesta ordem formam ou não uma proporção.
Temos então:
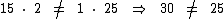
Como 30 difere de 25, não temos uma igualdade, consequentemente não temos uma proporção.
Poderíamos também ter analisado as duas razões:
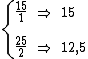
Como as duas razões possuem valores diferentes, obviamente não se trata de uma proporção.
 Como uma das razões resulta em 15 e a outra resulta em 12,5, concluímos que não se trata de uma proporção, já que 15 difere de 12,5.
Como uma das razões resulta em 15 e a outra resulta em 12,5, concluímos que não se trata de uma proporção, já que 15 difere de 12,5.
A proporção não ocorreu porque ao comprar 2kg de carne, eu obteria um desconto de R$ 2,50 no preço do quilograma, o que deixaria as razões desproporcionais.
 A soma de dois números é igual a 240. Sabe-se que um deles está para 5, assim como o outro está para 7. Quais são estes números?
A soma de dois números é igual a 240. Sabe-se que um deles está para 5, assim como o outro está para 7. Quais são estes números?
Para a resolução deste exemplo utilizaremos a terceira propriedade das proporções. Chamando um dos números de a e o outro de b, podemos montar a seguinte proporção:
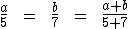
Sabemos que a soma de a com b resulta em 240, assim como a adição de 5 a 7 resulta em 12. Substituindo estes valores na proporção teremos:
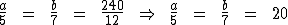
Portanto:
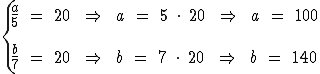
 Concluímos então que os dois números são 100 e 140.
Concluímos então que os dois números são 100 e 140.
 Quatro números, todos diferentes de zero, 10, 8, 25 e x formam nesta ordem uma proporção. Qual o valor de x?
Quatro números, todos diferentes de zero, 10, 8, 25 e x formam nesta ordem uma proporção. Qual o valor de x?
Seguindo o explicado sobre a quarta proporcional temos:
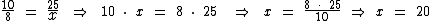
 O valor do número x é 20.
O valor do número x é 20.
