Mínimo Múltiplo Comum - MMC
Dados dois ou mais números naturais não nulos, denomina-se mínimo múltiplo comum (MMC) o menor dos seus múltiplos que é comum a todos eles, com exceção do número zero, pois este é menor dos números naturais e é múltiplo de todos eles.
Os múltiplos de um número natural são todos aqueles que divididos por este número têm zero como o resto da divisão. Por exemplo, 0, 6 e 12 são todos múltiplos de 6, pois qualquer um deles pode dividido por 6 em uma divisão exata. Neste caso o quociente da divisão seria respectivamente 0, 1 e 2. Percebe-se portanto, que os múltiplos de um número natural são o resultado do produto deste número por um outro número natural.
Já que o conjunto dos números naturais é um conjunto infinito, os múltiplos de um número também são infinitos.
Múltiplos de um Número Natural e o seu MMC
Tomemos por exemplo os números naturais 6, 8 e 12. Seus múltiplos são respectivamente:
- { 0, 6, 12, 18, 24, 30, ... }
- { 0, 8, 16, 24, 32, 40, ... }
- { 0, 12, 24, 36, 48, 60, ... }
Podemos notar que com exceção do número 0, o número 24 é o menor dos múltiplos comum a todos eles.
Temos então que:
MMC(6, 8, 12) = 24
Como descobrir o MMC de um conjunto de números?
Um prático método para se determinar o MMC de um conjunto de números naturais é a decomposição em fatores primos.
Para que possamos fazer uma comparação, vamos tomar novamente os números 6, 8 e 12 como exemplo.
Tópico relacionadoDecomposição de um Número Natural em Fatores Primos
Da fatoração destes três números temos:
- 6 = 2 . 3
- 8 = 23
- 12 = 22 . 3
O MMC(6, 8, 12) é o produto dos fatores comuns e não comuns, com os maiores expoentes.
O fator 2 é comum a todos eles, mas tomemos o 23, pois é o que possui o maior expoente.
O fator 3 não é comum ao número 8, mas independente disto também deve ser considerado e como nos dois casos onde ele é múltiplo, o expoente é 1, iremos considerar somente o 3 mesmo.
Note que cada fator é considerado apenas uma vez. O fator 3, por exemplo, ocorre tanto para o número 6, quanto para o números 12, mas o consideramos apenas uma vez.
Logo:
MMC(6, 8, 12) = 23 . 3 = 24
Propriedade do MMC e do MDC
Sejam a e b dois ou mais números naturais não nulos temos que MMC(a, b) . MDC(a, b) = a . b.
Observe que esta propriedade e válida apenas para o MMC/MDC entre exatamente dois números, para três números ou mais esta propriedade não se verifica.
Exemplos de MMC
 Qual é o MMC(15, 25, 40)?
Qual é o MMC(15, 25, 40)?
Fatorando os três números temos:
- 15 = 3 . 5
- 25 = 52
- 40 = 23 . 5
Para uma melhor identificação, os fatores comuns e não comuns com os maiores expoentes foram marcados em vermelho.
MMC(15, 25, 40) = 23 . 3 . 52 = 600
Portanto:
 O MMC(15, 25, 40) é igual 600
O MMC(15, 25, 40) é igual 600
 Qual é o MMC(250, 225, 294, 245)?
Qual é o MMC(250, 225, 294, 245)?
Da Fatoração dos quatro números temos:
- 250 = 2 . 53
- 225 = 32 . 52
- 294 = 2 . 3 . 72
- 245 = 5 . 72
MMC(250, 225, 294, 245) = 2 . 32 . 53 . 72 = 110250
Logo:
 O MMC(250, 225, 294, 245) é igual a 110250
O MMC(250, 225, 294, 245) é igual a 110250
 Qual é o MMC(27, 81)?
Qual é o MMC(27, 81)?
A decomposição dos dois números em fatores primos nos dá:
MMC(27, 81) = 34 = 81
Portanto:
 O MMC(27, 81) é o próprio número 81.
O MMC(27, 81) é o próprio número 81.
 Se o MDC(27, 72) = 9, qual é o MMC(27, 72)?
Se o MDC(27, 72) = 9, qual é o MMC(27, 72)?
Segundo a propriedade do MMC e do MDC temos que :
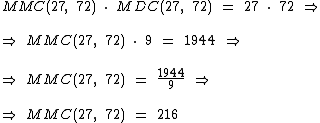
Logo:
 O MMC(27, 72) é igual a 216.
O MMC(27, 72) é igual a 216.
