Taxas Nominais

Você vai ao banco investir R$ 100.000,00 em uma aplicação financeira e o gerente lhe informa que para a aplicação escolhida a taxa de juros anual é de 24% a.a., com capitalização composta mensal.

Então você terá uma aplicação no regime de capitalização composta, sendo que o acréscimo dos juros ao montante será realizado mensalmente.

Note que o período de formação e acréscimo dos juros ao capital difere do período de tempo da taxa. Temos uma taxa anual, mas os juros são calculados e acrescidos mês a mês. Nestas condições a taxa de juros é denominada taxa nominal.

Tópico relacionadoExercícios resolvidos - Juros Compostos e Prestações

Sendo a taxa nominal de 24% a.a. e visto que a capitalização é mensal, qual será a taxa de juros ao mês?

Como 1 ano tem 12 meses a taxa será de:

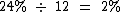
A taxa mensal referente a uma taxa nominal de 24% a.a. é de 2% a.m..

Estas duas taxas são ditas taxas proporcionais, pois utilizando meses como a unidade de tempo, temos a seguinte proporção:

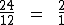
24% está para 12 meses, assim como 2% está 1 mês.

A taxa de 2% a.m. além de ser proporcional à taxa de 24% a.a., é denominada taxa efetiva mensal.

Taxas Efetivas

Segundo o dicionário efetiva significa real, verdadeira, que produz efeito. Isto quer dizer que para efeitos de cálculo utilizamos a taxa efetiva, a taxa nominal não é utilizada para estes fins.

Para continuarmos este estudo, agora que sabemos que a taxa efetiva de juros é 2% a.m. e que o capital é de R$ 100.000,00, vamos calcular qual será o novo capital após um ano de aplicação.

Vamos utilizar a seguinte fórmula para o cálculo do montante composto:

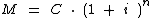
As variáveis conhecidas são as seguintes:

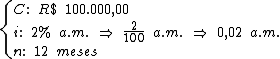
Substituindo tais variáveis por seus respectivos valores temos:

Como o capital é de R$ 100.000,00, os juros serão de R$ 26.824,18:

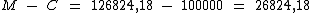
Então a taxa efetiva anual será de 26,82418% a.a.

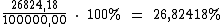
Taxas Equivalentes

A taxa efetiva mensal de 2% a.m. é equivalente à taxa efetiva anual de 26,82418% a.a., isto porque produzem um montante igual, quando aplicadas a um mesmo capital, em um período de tempo de mesma duração.

Para verificarmos a equivalência vamos calcular M_m e M_a, referentes ao montante obtido a partir das taxas efetivas mensal e anual, respectivamente, pelo período de um ano:

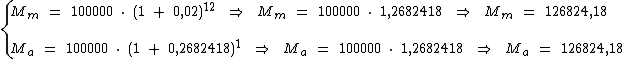
Observe que calculamos a taxa efetiva anual de 26,82418% a.a. com 5 casas decimais, apenas para que pudéssemos comparar a equivalência das taxas, na prática podemos utilizar uma ou duas casas decimais como 26,82% a.a., por exemplo, neste caso o montante será ligeiramente menor (R$ 126.820,00).

Acima verificamos que os montantes M_m e M_a, calculados através da fórmula 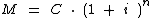, são iguais. Utilizando o índice m e a para identificar também as outras variáveis referentes ao cálculo dos montantes M_m e M_a, respectivamente, generalizando podemos concluir que:

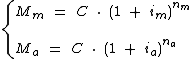
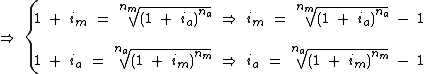
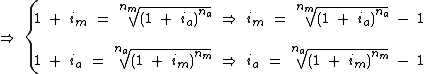
Veja que nesta fórmula obtemos a taxa efetiva mensal a partir da taxa efetiva anual:

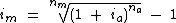
Nesta outra fórmula obtemos a taxa efetiva anual a partir da taxa efetiva mensal:

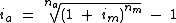
Como podemos notar, ambas as fórmulas diferem entre si apenas nos índices das variáveis, então retirando o índice das variáveis referentes à taxa que queremos obter e atribuindo o índice 0 às variáveis referentes à taxa que possuímos, chegamos à seguinte fórmula:

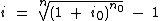
Ou, se preferirmos eliminar o radical trabalhando apenas com uma potência, temos esta fórmula:

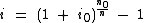
Exemplos de Cálculo para a Obtenção de Taxas Efetivas Equivalentes

A taxa efetiva de 21% a.a. equivale a qual taxa efetiva mensal?

Um capital qualquer capitalizado em 21% após 1 ano da aplicação, deve produzir o mesmo montante que o mesmo capital sendo capitalizado mensalmente a uma taxa i por 12 meses.

Os dados que possuímos são os seguintes:

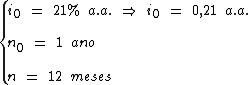
Substituindo tais valores na fórmula iremos obter a taxa efetiva ao mês:

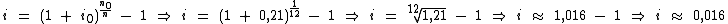
Portanto, a taxa efetiva mensal é de aproximadamente 0,016 a.m. ou 1,6% a.m.:

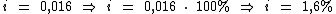
A taxa efetiva de 21% a.a. equivale a uma taxa efetiva mensal de 1,6% a.m.

A taxa efetiva de 1,8% a.b. equivale a qual taxa efetiva semestral?

Uma certa quantia capitalizada bimestralmente em 1,8% durante 3 bimestres de aplicação, deve produzir o mesmo montante se for capitalizada após 1 semestre a uma taxa i.

Então temos os seguintes dados para utilizar com a fórmula:

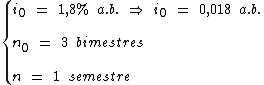
Os aplicando na fórmula temos:

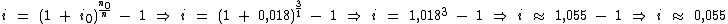
Temos então uma taxa efetiva semestral de aproximadamente 0,055 a.s. ou 5,5% a.s.:

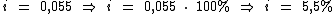
A taxa efetiva de 1,8% a.b. equivale a uma taxa efetiva semestral de 5,5% a.s.

Taxas Proporcionais

Vimos acima que as taxas de 24% a.a. e de 2% a.m. são taxas proporcionais, pois utilizando meses como a unidade de tempo, temos a seguinte proporção:

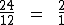
É importante observar que no regime de capitalização composta taxas proporcionais não são equivalentes. Como vimos, uma taxa efetiva de 2% a.m. equivale a 26,82418% a.a. e não a 24% a.a.

Note porém, que no regime de capitalização simples taxas proporcionais são equivalentes, neste regime elas produzem o mesmo montante quando aplicadas a um mesmo capital e período.

A taxa de 24% a.a. equivale à taxa de 2% a.m. em uma aplicação a juros simples?

Certamente que sim, por exemplo, vamos verificar o rendimento de uma aplicação de R$ 8.000,00 por 6 meses.

Para isto utilizaremos esta fórmula:

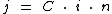
À taxa de 24% a.a. temos:

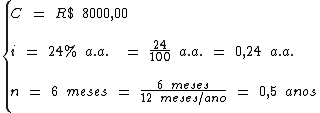
Como a taxa de juros está em anos e o período de aplicação em meses, foi preciso convertê-lo de 6 meses para 0,5 anos, a fim de que a unidade de tempo sendo a mesma, possamos realizar os cálculos:

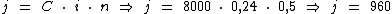
À taxa de 2% a.m. temos:

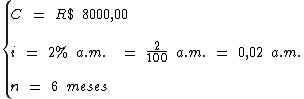
Portanto:

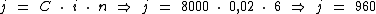
A aplicação de R$ 8.000,00 por 6 meses em qualquer uma das taxas proporcionais, rende juros de R$ 960,00 no regime de capitalização simples, portanto ambas as aplicações produzem o mesmo montante de R$ 8.960,00 durante um mesmo período de aplicação e por isto as taxas proporcionais são taxas equivalentes neste regime.

Sim, a taxa de 24% a.a. equivale à taxa de 2% a.m. no regime de capitalzação simples.