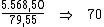Para maiores informações teóricas sobre este assunto veja também:Teoria - Juros simples
Exercícios resolvidos - Juros simples - Parte 2
21) Um investidor aplicou R$ 700.000,00 por 24 meses, à taxa de
juros simples de 49,44% a.a. Em quanto o capital foi aumentado por este
investimento?
Veja que neste caso a taxa de juros e o período não estão na mesma unidade de
tempo. Neste caso, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
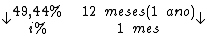
Resolvendo:
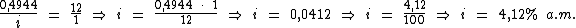
Identificando-se os termos disponíveis, temos:
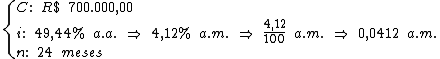
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
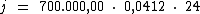
Logo:
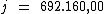
Portanto:
Com investimento o capital aumentou R$ 692.160,00.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
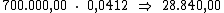
Ora, sendo o valor do juro em cada período correspondente a R$ 28.840,00,
resta-nos multiplicar este valor por 24, correspondente ao período de tempo,
para termos o valor procurado:
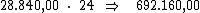
22) Minha aplicação rendeu de juros R$ 21,60. O dinheiro ficou
aplicado por 20 dias. Eu havia aplicado R$ 1.800,00. Qual foi a taxa
de juros a.b. da aplicação?
Identificando-se as variáveis disponíveis, temos:
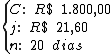
Para calcularmos a taxa de juros utilizaremos a fórmula:
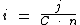
Substituindo o valor dos termos temos:
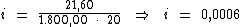
No entanto, como a unidade de tempo da taxa solicitada está em bimestres
('a.b.') e o cálculo foi realizado na unidade do período de tempo que está em
'dias', devemos converter a unidade de tempo da taxa calculada de a.d. ('dias')
para a.b. ('bimestres').
Logo:
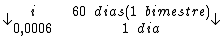
Resolvendo:
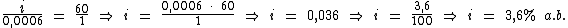
Portanto:
3,6% a.b. foi a taxa de juros simples da aplicação.
Alternativamente poderíamos dividir o valor total dos juros, R$ 21,60,
pelo valor do principal, R$ 1.800,00, de forma a encontrar a taxa de juros
total do período:
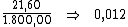
Dividindo-se então, esta taxa de 0,012 pelo período de tempo, 20, obteríamos a
taxa desejada:
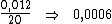
Resta ainda converter a taxa de juros para a unidade de tempo solicitada, o que
pode ser feito se realizando o procedimento de conversão conforme efetuado
acima.
23) Anita realizou uma aplicação por um período de 1 semestre. Em tal
período o capital de R$ 8.000,00 rendeu a ela R$ 880,00 de juros.
Qual foi a taxa de juros a.t. utilizada?
Veja bem que neste caso a taxa de juros e o período não estão na mesma unidade
de tempo. Sendo assim, devemos converter uma das unidades.
Identificando-se os termos disponíveis, temos:
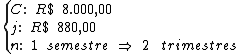
Para calcularmos a taxa de juros utilizaremos a fórmula:
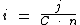
Substituindo o valor dos termos temos:
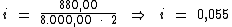
Logo:
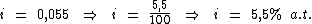
Portanto:
A aplicação foi realizada à uma taxa de juros simples de 5,5% a.t.
Alternativamente poderíamos dividir o valor total dos juros, R$ 880,00,
pelo valor do principal, R$ 8.000,00, de maneira a encontrar a taxa de
juros total do período:
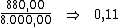
Dividindo-se então, esta taxa de 0,11 pelo período de tempo, 2, obteríamos a
taxa desejada:
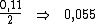
24) O Sr. Gouveia recebeu R$ 5.000,00 de juros, por um empréstimo de
10 dias. A taxa de juros aplicada foi de 7,5% a.m. Quanto o Sr.
Gouveia havia emprestado?
Esteja atento que neste caso a taxa de juros e o período não estão na mesma
unidade de tempo. Quando isto acontece, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
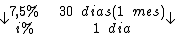
Resolvendo:
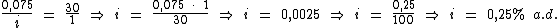
Identificando-se as variáveis disponíveis, temos:
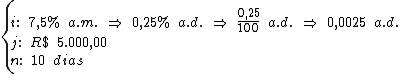
Para calcularmos o capital vamos utilizar a fórmula:
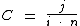
Substituindo o valor dos termos temos:
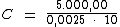
Logo:
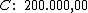
Portanto:
O Sr. Gouveia havia emprestado R$ 200.000,00, pelo qual recebeu
R$ 5.000,00 de juros, à taxa de 7,5% a.m. pelo período de
10 dias.
Poderíamos chegar à mesma conclusão pela seguinte forma:
Se dividirmos o valor total dos juros pelo período de tempo, iremos obter o
valor do juro por período:
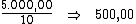
Portanto, ao dividirmos o valor do juro por período, R$ 500,00, pela taxa
de juros de 0,25%, iremos obter o valor do capital:
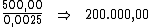
25) Fulano recebeu R$ 6.300,00 de juros ao aplicar R$ 70.000,00
à taxa de 36% a.a. Qual foi o prazo da aplicação em meses?
Veja que neste caso a taxa de juros e o período não estão na mesma unidade de
tempo. Neste caso, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
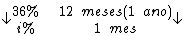
Resolvendo:
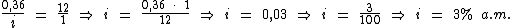
Identificando-se os termos disponíveis, temos:
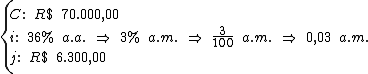
Para calcularmos o período de tempo utilizaremos a fórmula:
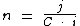
Substituindo o valor dos termos temos:
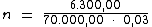
Logo:
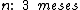
Portanto:
O prazo da aplicação foi de 3 meses. Aplicação esta que rendeu a Fulano
R$ 6.300,00 de juros ao investir R$ 70.000,00 à taxa de 36% a.a.
Sem utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, pelo seguinte
raciocínio:
Ao multiplicarmos o valor do capital pela taxa de juros, iremos obter o juro
referente a cada período:
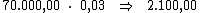
Neste caso, basta-nos dividir o valor de R$ 6.300,00, referente ao valor
total do juro, por R$ 2.100,00 correspondente ao valor do juro em cada
período, obtendo assim o período de tempo procurado:
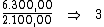
26) Calcule o montante e os juros referentes a um capital de
R$ 425.607,00 investido a 8,5% a.t., durante 7 semestres.
Observe que neste caso a taxa de juros e o período não estão na mesma unidade
de tempo. Nestas condições, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
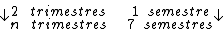
Resolvendo:
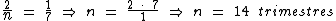
Identificando-se as variáveis disponíveis, temos:
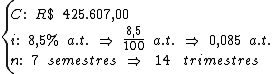
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
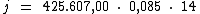
Logo:
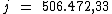
O montante é obtido somando-se ao valor do capital, o valor total dos juros.
Tal como na fórmula:
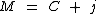
Ao substituirmos o valor das variáveis temos:
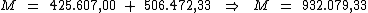
Portanto:
Ao aplicarmos um capital de R$ 425.607,00 investido a 8,5% a.t.,
durante 7 semestres, obteremos um juro total de R$ 506.472,33 e um
montante de R$ 932.079,33.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
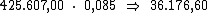
Ora, sendo o valor do juro em cada período correspondente a R$ 36.176,60,
resta-nos multiplicar este valor por 14, correspondente ao período de tempo,
para termos o valor procurado:
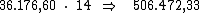
O valor do montante será encontrado, simplesmente somando-se ao valor do
principal, o valor total dos juros:
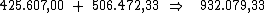
27) Prudêncio tomou emprestado R$ 97.000,00, pagando durante
3 anos, à taxa de juros simples de 5,4% a.s. Qual o juro resultante
após os 3 anos?
Veja bem que neste caso a taxa de juros e o período não estão na mesma unidade
de tempo. Sendo assim, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
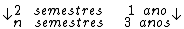
Resolvendo:
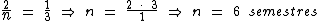
Identificando-se os termos disponíveis, temos:
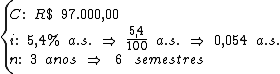
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
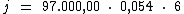
Logo:
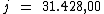
Portanto:
Ao tomar emprestado R$ 97.000,00 à taxa de juros simples de
5,4% a.s., por 3 anos Prudêncio pagará de juros um total de
R$ 31.428,00.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
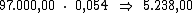
Ora, sendo o valor do juro em cada período correspondente a R$ 5.238,00,
resta-nos multiplicar este valor por 6, correspondente ao período de tempo,
para termos o valor procurado:
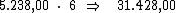
28) Para comprar sementes, adubos e pesticidas, um pequeno agricultor
realizou um empréstimo a uma taxa de juros simples de 1,5% a.b. Sabe-se
que a duração do empréstimo foi de 10 meses, qual o juro pago para um
empréstimo de R$ 150.000,00?
Esteja atento que neste caso a taxa de juros e o período não estão na mesma
unidade de tempo. Quando isto acontece, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
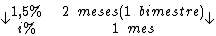
Resolvendo:
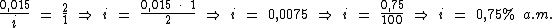
Identificando-se as variáveis disponíveis, temos:
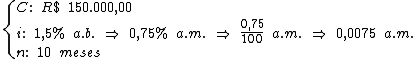
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
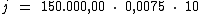
Logo:
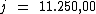
Portanto:
O capital de R$ 150.000,00 emprestado a 1,5% a.b., durante
10 meses resultou em um juro total de R$ 11.250,00.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
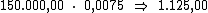
Ora, sendo o valor do juro em cada período correspondente a R$ 1.125,00,
resta-nos multiplicar este valor por 10, correspondente ao período de tempo,
para termos o valor procurado:
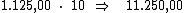
29) Qual o valor dos juros e do montante resultantes de um empréstimo de
R$ 29.000,00 feito pelo prazo de 4 meses, à taxa de 1,75% a.m.?
Identificando-se os termos disponíveis, temos:
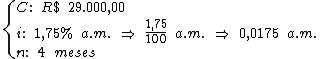
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
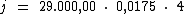
Logo:
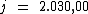
O montante é obtido somando-se ao valor do capital, o valor total dos juros.
Tal como na fórmula:
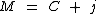
Ao substituirmos o valor dos termos temos:
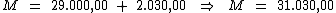
Portanto:
O valor dos juros será de R$ 2.030,00, resultante do empréstimo de
R$ 29.000,00 à taxa de 1,75% a.m., pelo prazo de 4 meses. O
montante será de R$ 31.030,00.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
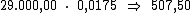
Ora, sendo o valor do juro em cada período correspondente a R$ 507,50,
resta-nos multiplicar este valor por 4, correspondente ao período de tempo,
para termos o valor procurado:
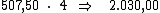
O valor do montante será encontrado, simplesmente somando-se ao valor do
principal, o valor total dos juros:
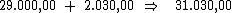
30) Qual o valor dos juros correspondente a um empréstimo de
R$ 122.000,00 realizado pelo prazo de 3 bimestres, à taxa de
19,2% a.s.?
Observe que neste caso a taxa de juros e o período não estão na mesma unidade
de tempo. Nestas condições, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
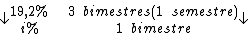
Resolvendo:
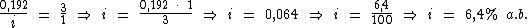
Identificando-se as variáveis disponíveis, temos:
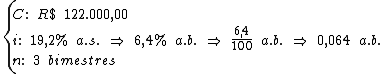
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
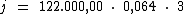
Logo:
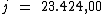
Portanto:
O valor dos juros será de R$ 23.424,00, correspondente ao empréstimo de
R$ 122.000,00 à taxa de 19,2% a.s., pelo prazo de 3 bimestres.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
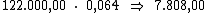
Ora, sendo o valor do juro em cada período correspondente a R$ 7.808,00,
resta-nos multiplicar este valor por 3, correspondente ao período de tempo,
para termos o valor procurado:
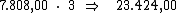
31) Vendi uma lancha pela qual receberei R$ 219.300,00, dos quais
R$ 69.300,00 se referem aos juros, a uma taxa de 6,6% a.t. Por
quantos trimestres eu receberei as prestações pela venda desta lancha?
Qual o preço dela sem os juros?
Primeiramente iremos calcular o valor do capital.
A diferença entre o montante (R$ 219.300,00) e o valor total do juro
(R$ 69.300,00), nos dá o valor do capital:
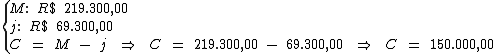
Identificando-se os termos disponíveis, temos:
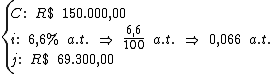
Para calcularmos o período de tempo utilizaremos a fórmula:
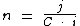
Substituindo o valor dos termos temos:
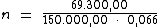
Logo:
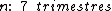
Portanto:
O valor de venda da lancha sem os juros é de R$ 150.000,00 e o prazo para
o recebimento é de 7 trimestres.
Sem utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, pelo seguinte
raciocínio:
Ao multiplicarmos o valor do capital pela taxa de juros, iremos obter o juro
referente a cada período:
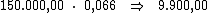
Neste caso, basta-nos dividir o valor de R$ 69.300,00, referente ao valor
total do juro, por R$ 9.900,00 correspondente ao valor do juro em cada
período, obtendo assim o período de tempo procurado:
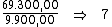
32) Flávia comprou uma motocicleta, a prazo, pagando um total de
R$ 15.286,72. O seu valor à vista é de R$ 12.400,00 e a taxa de juros
é de 0,97% a.m. Por quantos anos Flávia ficará com esta dívida?
Em primeiro lugar, devemos calcular o valor do juro total.
Obtemos o valor do juro total ao subtrairmos do montante
(R$ 15.286,72), o valor do capital (R$ 12.400,00):
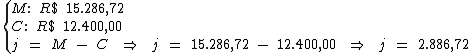
Esteja atento que neste caso a taxa de juros e o período não estão na mesma
unidade de tempo. Quando isto acontece, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
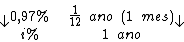
Resolvendo:
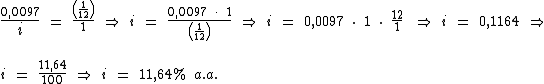
Identificando-se as variáveis disponíveis, temos:
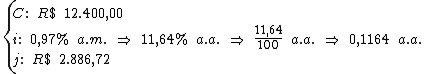
Para calcularmos o período de tempo utilizaremos a fórmula:
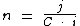
Substituindo o valor dos termos temos:
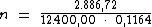
Logo:
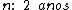
Portanto:
Flávia ficará pagando a sua motocicleta por 2 anos.
Sem utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, pelo seguinte
raciocínio:
Ao multiplicarmos o valor do capital pela taxa de juros, iremos obter o juro
referente a cada período:
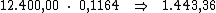
Desta forma, basta-nos dividir o valor de R$ 2.886,72, referente ao valor
total do juro, por R$ 1.443,36 correspondente ao valor do juro em cada
período, obtendo assim o período de tempo procurado:
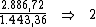
33) Beatriz resgatou R$ 10.201,84 de uma aplicação, após decorridos
3 trimestres. O valor dos juros obtidos foi de R$ 1.401,84. Qual a
taxa de juros a.m.?
Inicialmente o valor do capital será obtido subtraindo-se do montante
(R$ 10.201,84), o valor total do juro (R$ 1.401,84):
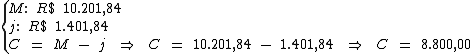
Veja que neste caso a taxa de juros e o período não estão na mesma unidade de
tempo. Neste caso, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
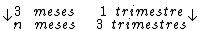
Resolvendo:
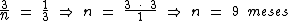
Identificando-se os termos disponíveis, temos:
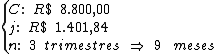
Para calcularmos a taxa de juros utilizaremos a fórmula:
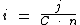
Substituindo o valor dos termos temos:
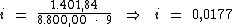
Logo:
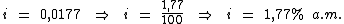
Portanto:
1,77% a.m. é a taxa de juros da aplicação resgatada por Beatriz.
Alternativamente poderíamos dividir o valor total dos juros, R$ 1.401,84,
pelo valor do principal, R$ 8.800,00, de sorte a encontrar a taxa de juros
total do período:
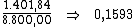
Dividindo-se então, esta taxa de 0,1593 pelo período de tempo, 9, obteríamos a
taxa desejada:
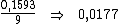
34) O valor principal de uma aplicação é de R$ 65.400,00. Resgatou-se
um total de R$ 83.450,40 em 1 ano. Qual o valor dos juros e a sua
respectiva taxa a.t.?
Para começar, devemos calcular o valor do juro total subtraindo-se do montante
(R$ 83.450,40), o valor do capital (R$ 65.400,00):
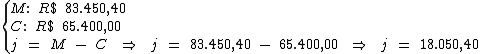
Observe que neste caso a taxa de juros e o período não estão na mesma unidade
de tempo. Nestas condições, devemos converter uma das unidades.
Identificando-se as variáveis disponíveis, temos:
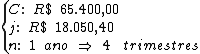
Para calcularmos a taxa de juros utilizaremos a fórmula:
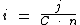
Substituindo o valor dos termos temos:
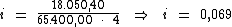
Logo:
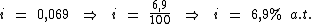
Portanto:
A taxa de juros da aplicação resgatada é de 6,9% a.t. O valor dos juros é
de R$ 18.050,40.
Alternativamente poderíamos dividir o valor total dos juros, R$ 18.050,40,
pelo valor do principal, R$ 65.400,00, de forma a encontrar a taxa de
juros total do período:
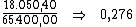
Dividindo-se então, esta taxa de 0,276 pelo período de tempo, 4, obteríamos a
taxa desejada:
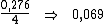
35) Marcelo comprou um aparelho de som que custa R$ 3.500,00, a uma
taxa de juros simples de 1,98% a.m., pelo período de 2 anos. Qual o
valor total a pagar? Qual o valor dos juros?
Veja bem que neste caso a taxa de juros e o período não estão na mesma unidade
de tempo. Sendo assim, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
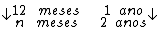
Resolvendo:
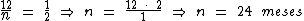
Identificando-se os termos disponíveis, temos:
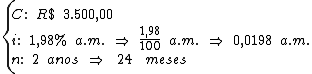
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
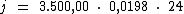
Logo:
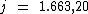
O montante é obtido somando-se ao valor do capital, o valor total dos juros.
Tal como na fórmula:
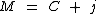
Ao substituirmos o valor dos termos temos:
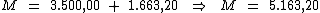
Portanto:
O valor dos juros será de R$ 1.663,20, que acrescentado ao preço do
aparelho de R$ 3.500,00, irá totalizar R$ 5.163,20.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
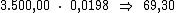
Ora, sendo o valor do juro em cada período correspondente a R$ 69,30,
resta-nos multiplicar este valor por 24, correspondente ao período de tempo,
para termos o valor procurado:
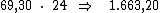
O valor do montante será encontrado, simplesmente somando-se ao valor do
principal, o valor total dos juros:
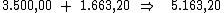
36) Eduardo e Mônica investiram R$ 100.000,00 por 30 bimestres,
à taxa de juros simples de 6% a.a., para os estudos de seu filho único. Em
quanto o capital foi aumentado por este investimento?
Esteja atento que neste caso a taxa de juros e o período não estão na mesma
unidade de tempo. Quando isto acontece, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
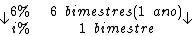
Resolvendo:
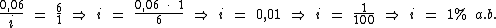
Identificando-se as variáveis disponíveis, temos:
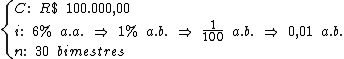
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
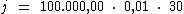
Logo:
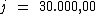
Portanto:
Com investimento o valor principal aumentou R$ 30.000,00.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
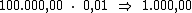
Ora, sendo o valor do juro em cada período correspondente a R$ 1.000,00,
resta-nos multiplicar este valor por 30, correspondente ao período de tempo,
para termos o valor procurado:
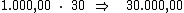
37) Saquei os R$ 38,25 de juros que minha aplicação rendeu. O
dinheiro ficou investido por 45 dias. Eu havia aplicado R$ 5.000,00.
Qual foi a taxa de juros a.m. da aplicação?
Identificando-se os termos disponíveis, temos:
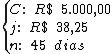
Para calcularmos a taxa de juros utilizaremos a fórmula:
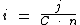
Substituindo o valor dos termos temos:
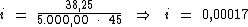
No entanto, como a unidade de tempo da taxa solicitada está em meses ('a.m.') e
o cálculo foi realizado na unidade do período de tempo que está em 'dias',
devemos converter a unidade de tempo da taxa calculada de a.d. ('dias') para
a.m. ('meses').
Logo:
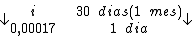
Resolvendo:
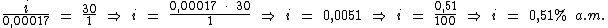
Portanto:
0,51% a.m. foi a taxa de juros simples desta aplicação.
Alternativamente poderíamos dividir o valor total dos juros, R$ 38,25,
pelo valor do principal, R$ 5.000,00, de forma a encontrar a taxa de juros
total do período:
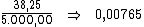
Dividindo-se então, esta taxa de 0,00765 pelo período de tempo, 45, obteríamos
a taxa desejada:
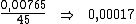
Resta ainda converter a taxa de juros para a unidade de tempo solicitada, o que
pode ser feito se realizando o procedimento de conversão conforme efetuado
acima.
38) Marcelinho realizou uma aplicação por um período de 1 ano. Em tal
período o principal de R$ 7.250,00 rendeu a ele R$ 765,60 de juros.
Qual foi a taxa de juros a.b. utilizada?
Observe que neste caso a taxa de juros e o período não estão na mesma unidade
de tempo. Nestas condições, devemos converter uma das unidades.
Identificando-se as variáveis disponíveis, temos:
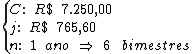
Para calcularmos a taxa de juros utilizaremos a fórmula:
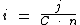
Substituindo o valor dos termos temos:
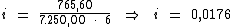
Logo:
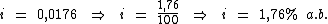
Portanto:
A aplicação foi realizada à uma taxa de juros simples de 1,76% a.b.
Alternativamente poderíamos dividir o valor total dos juros, R$ 765,60,
pelo valor do principal, R$ 7.250,00, de maneira a encontrar a taxa de
juros total do período:
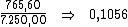
Dividindo-se então, esta taxa de 0,1056 pelo período de tempo, 6, obteríamos a
taxa desejada:
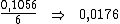
39) Rogério recebeu R$ 2.231,60 de juros, por um empréstimo de
20 dias. A taxa de juros aplicada foi de 6,3% a.m. Quanto Rogério
havia emprestado?
Veja bem que neste caso a taxa de juros e o período não estão na mesma unidade
de tempo. Sendo assim, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
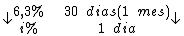
Resolvendo:
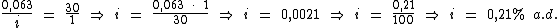
Identificando-se os termos disponíveis, temos:
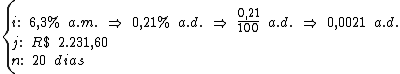
Para calcularmos o capital vamos utilizar a fórmula:
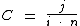
Substituindo o valor dos termos temos:
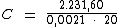
Logo:
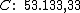
Portanto:
Rogério havia emprestado R$ 53.133,33, pelo qual recebeu R$ 2.231,60
de juros, à taxa de 6,3% a.m. pelo período de 20 dias.
Poderíamos chegar à mesma conclusão pela seguinte forma:
Se dividirmos o valor total dos juros pelo período de tempo, iremos obter o
valor do juro por período:
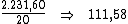
Portanto, ao dividirmos o valor do juro por período, R$ 111,58, pela taxa
de juros de 0,21%, iremos obter o valor do capital:
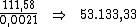
40) Solange recebeu R$ 5.568,50 de juros ao aplicar R$ 86.000,00
à taxa de 33,3% a.a. Qual foi o prazo da aplicação em dias?
Esteja atento que neste caso a taxa de juros e o período não estão na mesma
unidade de tempo. Quando isto acontece, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
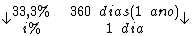
Resolvendo:
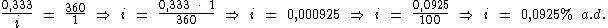
Identificando-se as variáveis disponíveis, temos:
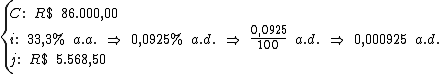
Para calcularmos o período de tempo utilizaremos a fórmula:
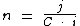
Substituindo o valor dos termos temos:
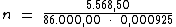
Logo:
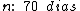
Portanto:
O prazo da aplicação foi de 70 dias. Aplicação esta que rendeu a Solange
R$ 5.568,50 de juros ao investir R$ 86.000,00 à taxa de
33,3% a.a.
Sem utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, pelo seguinte
raciocínio:
Ao multiplicarmos o valor do capital pela taxa de juros, iremos obter o juro
referente a cada período:
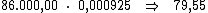
Neste caso, basta-nos dividir o valor de R$ 5.568,50, referente ao valor
total do juro, por R$ 79,55 correspondente ao valor do juro em cada
período, obtendo assim o período de tempo procurado:
