Quando estudamos o regime de capitalização de juros compostos, tínhamos a situação onde fazíamos um único depósito no início da aplicação e não realizávamos nenhum outro depósito durante todo o seu período. Neste tópico vamos tratar de investimentos com depósitos periódicos e iguais.
Para estudarmos este caso vamos utilizar uma aplicação exemplo onde iremos realizar 4 depósitos mensais de R$ 400,00 a uma taxa de juro composto de 2,5% a.m., sendo que realizaremos o resgate logo após o último depósito.
Para facilitar o entendimento vamos nos utilizar da tabela abaixo:
| | 1° mês | 2° mês | 3° mês | 4° mês |
| 1° depósito | R$ 400,00 | R$ 400,00 + 2,5% = R$ 410,00 | R$ 410,00 + 2,5% = R$ 420,25 | R$ 420,25 + 2,5% = R$ 430,76 |
| 2° depósito | | R$ 400,00 | R$ 400,00 + 2,5% = R$ 410,00 | R$ 410,00 + 2,5% = R$ 420,25 |
| 3° depósito | | | R$ 400,00 | R$ 400,00 + 2,5% = R$ 410,00 |
| 4° depósito | | | | R$ 400,00 |
| Valor a Resgatar | | | | R$ 1.661,01 |
|---|
Observe que cada depósito só sofre o acréscimo de juros ao término de cada mês. No caso do primeiro depósito haverá acréscimo de juros ao término do primeiro, segundo e terceiro mês, passando de R$ 400,00 a R$ 430,76.
Como você pode notar, a cada depósito o número de meses com acréscimo de juros diminui, obviamente porque temos menos períodos até o término da aplicação.
Como os juros são computados no início do próximo período, obviamente o quarto depósito não irá sofrer o acréscimo de juros, pois a aplicação será resgatada no início do quarto período, logo após o quarto depósito.
Fórmula de Cálculo do Valor Acumulado com Resgate ao Iniciar o Último Período
Neste caso o resgate será realizado logo após o último depósito, não sendo portanto computados juros referentes a este depósito, nem aos depósitos anteriores.
Para chegarmos ao valor resgatado de R$ 1.661,01 da situação acima, podemos recorrer à seguinte fórmula:
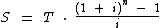
Onde:
- S: É o valor acumulado no período.
- T: É o valor de cada depósito periódico.
- i: É a taxa percentual aplicada ao capital para a apuração do juro.
- n: É o número de depósitos da aplicação.
O termo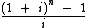 
também é conhecido como fator de acumulação de capital, representado pela variável s.
Podemos então obtê-lo através da seguinte fórmula:
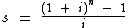
Abaixo temos identificadas as variáveis do nosso problema para calcularmos o valor acumulado no período:
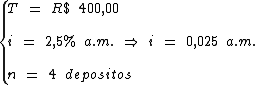
Basta-nos substituí-las na fórmula e executarmos os cálculos:
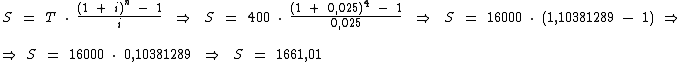
Chegamos então aos R$ 1.661,01 correspondentes à soma dos montantes dos três primeiros depósitos, mais o valor do quarto depósito, depósito este que não teve juros computados, mas qual seria a fórmula se tivéssemos computado os juros do quarto período?
Fórmula de Cálculo do Valor Acumulado com Resgate ao Terminar o Último Período
Neste outro caso o resgate se dará somente após o acréscimo dos juros referentes ao último depósito, assim como dos depósitos anteriores.
Para esta situação vamos utilizar a seguinte fórmula:
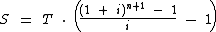
As variáveis são as mesmas do caso anterior. Ao substituí-las na fórmula e executarmos os cálculos temos:
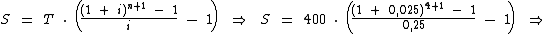
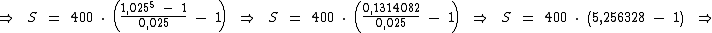
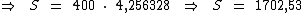
Veja que agora obtivemos um valor acumulado de R$ 1.702,53.
Podemos verificar o resultado obtido através da fórmula, calculando os juros resultantes imediatamente após o término do quarto período nos dados da tabela anterior:
| | 1° mês | 2° mês | 3° mês | 4° mês | Após o 4° mês |
| 1° depósito | R$ 400,00 | R$ 400,00 + 2,5% = R$ 410,00 | R$ 410,00 + 2,5% = R$ 420,25 | R$ 420,25 + 2,5% = R$ 430,76 | R$ 430,76 + 2,5% = R$ 441,53 |
| 2° depósito | | R$ 400,00 | R$ 400,00 + 2,5% = R$ 410,00 | R$ 410,00 + 2,5% = R$ 420,25 | R$ 420,25 + 2,5% = R$ 430,76 |
| 3° depósito | | | R$ 400,00 | R$ 400,00 + 2,5% = R$ 410,00 | R$ 410,00 + 2,5% = R$ 420,25 |
| 4° depósito | | | | R$ 400,00 | R$ 400,00 + 2,5% = R$ 410,00 |
| Valor a Resgatar | | | | | R$ 1.702,54 |
|---|
Note que a diferença de um centavo deve-se apenas ao erro de arredondamento resultante dos diferentes cálculos efetuados por um método e outro.
