Exercícios resolvidos - Juros compostos e Prestações
Para maiores informações teóricas sobre este assunto veja também:Teoria - Juros compostos
 1) Aplicando-se R$ 15.000,00 a uma taxa de juro composto de 1,7% a.m., quanto receberei de volta após um ano de aplicação? Qual o juro obtido neste período?
1) Aplicando-se R$ 15.000,00 a uma taxa de juro composto de 1,7% a.m., quanto receberei de volta após um ano de aplicação? Qual o juro obtido neste período?
Primeiramente vamos identificar cada uma das variáveis fornecidas pelo enunciado do problema:
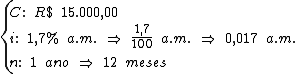
Como a taxa de juros está em meses, também iremos trabalhar com o período de tempo em meses e não em anos como está no enunciado do problema.
Pelo enunciado identificamos que foram solicitados o montante e o juro, utilizaremos, portanto a fórmula abaixo que nos dá o montante:

Ao substituirmos cada uma das variáveis pelo seu respectivo valor teremos:
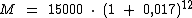
Podemos então realizar os cálculos para encontramos o valor do montante:

Logo o montante a receber será de R$ 18.362,96. Sabemos que a diferença entre o montante e o capital aplicado nos dará os juros do período. Temos então:
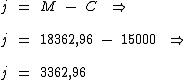
Portanto:
 Após um ano de aplicação receberei de volta um total de R$ 18.362,96, dos quais R$ 3.362,96 serão recebidos a título de juros.
Após um ano de aplicação receberei de volta um total de R$ 18.362,96, dos quais R$ 3.362,96 serão recebidos a título de juros.
 2) Paguei de juros um total R$ 2.447,22 por um empréstimo de 8 meses a uma taxa de juro composto de 1,4% a.m. Qual foi o capital tomado emprestado?
Tópico relacionadoCalculando o valor da entrada para financiar a compra do seu carro a partir do valor da prestação
2) Paguei de juros um total R$ 2.447,22 por um empréstimo de 8 meses a uma taxa de juro composto de 1,4% a.m. Qual foi o capital tomado emprestado?
Tópico relacionadoCalculando o valor da entrada para financiar a compra do seu carro a partir do valor da prestação
Em primeiro lugar vamos identificar as variáveis fornecidas pelo enunciado:
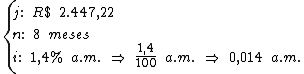
Como sabemos a fórmula básica para o cálculo do juro composto é:

Mas como estamos interessados em calcular o capital, é melhor que isolemos a variável C como a seguir:
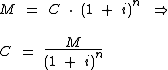
Note que a variável M não consta no enunciado, mas ao invés disto temos a variável j, no entanto sabemos que o valor do montante é igual à soma do valor principal com o juro do período, então temos:
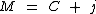
Podemos então substituir M por C + j na expressão anterior:
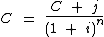
Vamos então novamente isolar a variável C:
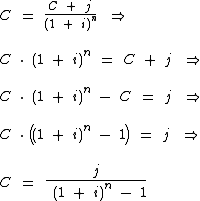
Finalmente podemos substituir as variáveis da fórmula pelos valores obtidos do enunciado:
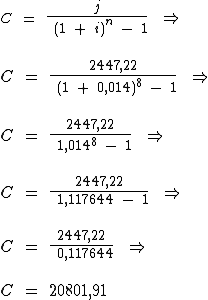
Logo:
 O capital tomado emprestado foi de R$ 20.801,96.
O capital tomado emprestado foi de R$ 20.801,96.
 3) Planejo emprestar R$ 18.000,00 por um período de 18 meses ao final do qual pretendo receber de volta um total de R$ 26.866,57. Qual deve ser o percentual da taxa de juro composto para que eu venha a conseguir este montante?
3) Planejo emprestar R$ 18.000,00 por um período de 18 meses ao final do qual pretendo receber de volta um total de R$ 26.866,57. Qual deve ser o percentual da taxa de juro composto para que eu venha a conseguir este montante?
Do enunciado identificamos as seguintes variáveis:
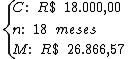
A partir da fórmula básica para o cálculo do juro composto iremos isolar a variável i, que se refere à taxa de juros que estamos em busca:

Como já vimos na parte teórica, esta variável pode ser isolada com os seguintes passos:
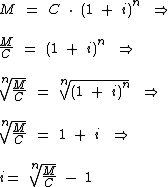
Por fim substituiremos as variáveis da fórmula pelos valores obtidos do enunciado:
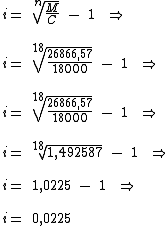
O valor decimal 0,0225 corresponde ao valor percentual de 2,25%.
Logo:
 Para que eu venha obter o montante desejado, é preciso que a taxa de juro composto seja de 2,25% a.m.
Para que eu venha obter o montante desejado, é preciso que a taxa de juro composto seja de 2,25% a.m.
 4) Preciso aplicar R$ 100.000,00 por um período de quantos meses, a uma taxa de juro composto de 1,7% a.m., para que ao final da aplicação eu obtenha o dobro deste capital?
4) Preciso aplicar R$ 100.000,00 por um período de quantos meses, a uma taxa de juro composto de 1,7% a.m., para que ao final da aplicação eu obtenha o dobro deste capital?
Do enunciado identificamos as seguintes variáveis:
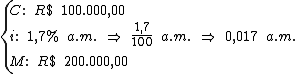
Tendo por base a fórmula básica para o cálculo do juro composto isolemos a variável n, que se refere ao período de tempo que estamos a procura:

Substituindo o valor das variáveis na fórmula:
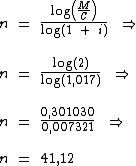
Assim sendo:
 Para que eu consiga dobrar o valor do meu capital precisarei de 41,12 meses de aplicação.
Para que eu consiga dobrar o valor do meu capital precisarei de 41,12 meses de aplicação.
 5) Se um certo capital for aplicado por um único período a uma determinada taxa de juros, em qual das modalidades de juros, simples ou composta, se obterá o maior rendimento?
5) Se um certo capital for aplicado por um único período a uma determinada taxa de juros, em qual das modalidades de juros, simples ou composta, se obterá o maior rendimento?
Na modalidade de juros simples, temos que o montante pode ser obtido através da seguinte fórmula:
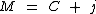
Mas como já sabemos, o juro é obtido através da fórmula:
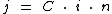
Logo substituindo j na fórmula do montante, chegamos à seguinte expressão:
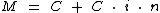
Que após colocarmos C em evidência teremos:
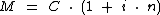
Como o enunciado diz se tratar de apenas um período de aplicação, ao substituirmos n por 1 e realizarmos a multiplicação, a fórmula ficará apenas como:
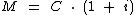
Já na modalidade de juros compostos, o montante é obtido através da fórmula:

Com a substituição de n por 1, segundo o enunciado, chegaremos à expressão:
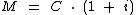
Como já era de se esperar, em ambas as modalidades chegamos à mesma fórmula. Por quê?
Como sabemos, o que difere uma modalidade da outra é que no caso dos juros simples o juro não é integrado ao capital ao final de cada período, assim como acontece na modalidade de juros compostos. Como há apenas um período, não há distinção entre uma modalidade e outra, já que após a integração do juro ao valor principal, não haverá um outro cálculo para um próximo período, por se tratar de apenas um período de aplicação.
Temos então que:
 Em qualquer uma das modalidades o rendimento será o mesmo.
Em qualquer uma das modalidades o rendimento será o mesmo.
 6) R$ 10.000,00 aplicados por 6 meses a uma taxa de juros simples de 3% a.m., para produzir o mesmo montante na modalidade de juros composto em um aplicação com a mesma duração, precisará ser aplicada a qual taxa mensal?
6) R$ 10.000,00 aplicados por 6 meses a uma taxa de juros simples de 3% a.m., para produzir o mesmo montante na modalidade de juros composto em um aplicação com a mesma duração, precisará ser aplicada a qual taxa mensal?
Do enunciado obtemos os seguintes valores:
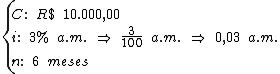
Para sabermos qual o montante produzido na modalidade simples utilizaremos a fórmula abaixo:
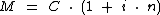
Ao substituirmos as variáveis e realizarmos os cálculos iremos obter o resultado:
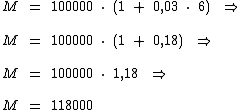
Agora que sabemos que o montante produzido na modalidade simples é R$ 11.800,00, utilizaremos a fórmula abaixo para calcularmos a taxa de juros na modalidade capitalizada:
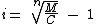
Substituindo as variáveis e calculando:
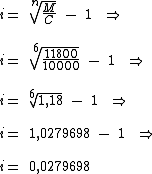
Como sabemos ao multiplicarmos 0,0279698 por cem iremos obter o valor percentual da taxa a qual estamos procurando.
Portanto:
 Os R$ 10.000,00 precisam ser aplicados à taxa capitalizada de 2,79698% a.m. para que se apure o montante de R$ 11.800,00, o mesmo montante produzido na aplicação a juros simples pelo mesmo período de tempo.
Os R$ 10.000,00 precisam ser aplicados à taxa capitalizada de 2,79698% a.m. para que se apure o montante de R$ 11.800,00, o mesmo montante produzido na aplicação a juros simples pelo mesmo período de tempo.
 7) Um aparelho DVD Player custa à vista R$ 250,00. Se pago sem entrada em 6 prestações mensais a uma taxa de juros de 3% a.m., qual será o valor de cada prestação mensal?
7) Um aparelho DVD Player custa à vista R$ 250,00. Se pago sem entrada em 6 prestações mensais a uma taxa de juros de 3% a.m., qual será o valor de cada prestação mensal?
Identificando as variáveis do problema temos:
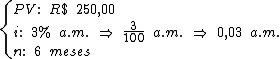
Calculemos então o coeficiente de financiamento:
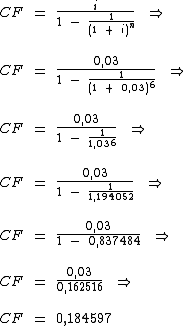
Agora que temos o coeficiente de financiamento podemos calcular o valor da prestação que é identificado pela variável PMT conforme a resolução através da fórmula abaixo:

Portanto:
 O valor da prestação mensal do DVD Player será de R$ 46,15.
O valor da prestação mensal do DVD Player será de R$ 46,15.
 8) Um eletrodoméstico sai à vista por R$ 550,00. Se for dada uma entrada de R$ 150,00 e o restante for pago em 4 prestações mensais a uma taxa de juros de 2,5% a.m., qual será o valor mensal de cada parcela?
8) Um eletrodoméstico sai à vista por R$ 550,00. Se for dada uma entrada de R$ 150,00 e o restante for pago em 4 prestações mensais a uma taxa de juros de 2,5% a.m., qual será o valor mensal de cada parcela?
Como iremos abater R$ 150,00 dos R$ 550,00 que é o valor do produto, acabaremos financiando apenas R$ 400,00. Portanto as variáveis do problema têm os seguintes valores:
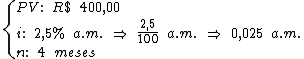
Agora podemos calcular o coeficiente de financiamento:
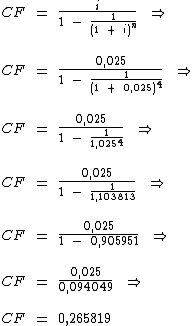
Aplicando a fórmula para o cálculo de prestações podemos executar os cálculos conforme abaixo:

Portanto:
 O valor mensal da prestação deste eletrodoméstico será de R$ 106,33.
O valor mensal da prestação deste eletrodoméstico será de R$ 106,33.
 9) Comprei um aparelho eletrônico que à vista custava R$ 1.250,00 dando uma entrada mais 3 prestações mensais de igual valor, a uma taxa de juros de 1,2% a.m. Qual o valor de cada pagamento?
9) Comprei um aparelho eletrônico que à vista custava R$ 1.250,00 dando uma entrada mais 3 prestações mensais de igual valor, a uma taxa de juros de 1,2% a.m. Qual o valor de cada pagamento?
Para o cálculo do valor das prestações com o mesmo valor da entrada, iremos utilizar esta fórmula:
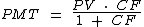
A partir do enunciado destacamos os seguintes valores para as variáveis:
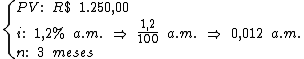
Segundo a fórmula acima, necessitamos do coeficiente de financiamento. Seu cálculo segue abaixo:
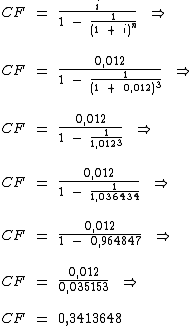
Substituindo-se os valores das variáveis na fórmula inicial temos:
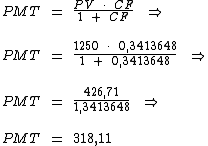
Portanto:
 O valor mensal da prestação deste eletrodoméstico, assim como o valor da sua entrada foi de R$ 318,11.
O valor mensal da prestação deste eletrodoméstico, assim como o valor da sua entrada foi de R$ 318,11.
 10) Um aparelho DVD Player foi pago em 5 prestações mensais de R$ 383,90 sem entrada. Sabendo-se que a taxa de juros foi de 2% a.m., qual seria o pago caso eu tivesse feito a compra à vista?
10) Um aparelho DVD Player foi pago em 5 prestações mensais de R$ 383,90 sem entrada. Sabendo-se que a taxa de juros foi de 2% a.m., qual seria o pago caso eu tivesse feito a compra à vista?
Para o cálculo de PV que corresponde ao valor à vista, utilizaremos a fórmula:
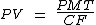
Para calcularmos o coeficiente de financiamento utilizaremos as variáveis a seguir:
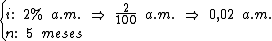
Vamos então calculá-lo:
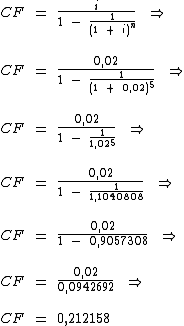
Sabendo-se que PMT = 383,90 e que CF = 0,212158, podemos calcular PV:
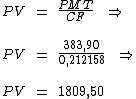
Portanto:
 Eu teria pago um total de R$ 1.809,50 se tivesse realizado a compra à vista.
Eu teria pago um total de R$ 1.809,50 se tivesse realizado a compra à vista.
