Uma coisa muito comum na vida de todos nós, pelo menos na vida da grande maioria da população brasileira, são as tão onipresentes prestações, visto que nem sempre possuímos a quantia necessária para realizarmos a compra à vista daquele bem tão imprescindível e principalmente por não termos a cultura de acumular mês a mês um certo valor, até totalizarmos o valor necessário.

Tópico relacionadoCalculando o valor da entrada para financiar a compra do seu carro a partir do valor da prestação

Quando não há na operação de compra, pelo menos de forma declarada, a cobrança de juros, basta que dividamos o valor da mercadoria pelo número de parcelas, para obtermos o valor de cada prestação, mas e no caso de haver incidência de juros, como podemos realizar os cálculos? Como podemos saber que não estamos sendo ludibriados por algum vendedor inescrupuloso?

Neste tópico iremos estudar o que é coeficiente de financiamento e como poderemos utilizá-lo no cálculo de prestações, assim como tendo o valor capitalizado, encontrarmos o valor à vista sem juros, por exemplo.

Coeficiente de Financiamento

O coeficiente de financiamento é um fator que ao ser multiplicado pelo valor a ser financiado, irá nos fornecer o valor de cada prestação.

O cálculo do coeficiente de financiamento tem como variáveis tanto a taxa de juros, quanto o número de períodos da operação. Ele é calculado através da seguinte fórmula:

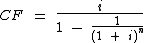
A variável CF representa o próprio coeficiente de financiamento, já as variáveis i e n representam respectivamente a taxa de juros cobrada pelo financiamento e o período ou número de parcelas mensais, já que quase invariavelmente as prestações são mensais.

Assim como nos cálculos envolvendo juros simples e juros compostos, no caso do cálculo de prestações tanto a taxa de financiamento, quanto o período, devem estar na mesma unidade de tempo. Como geralmente as prestações são mensais, a taxa de juros também deverá ser expressa ao mês.

Vejamos alguns exemplos de vendas envolvendo juros:

Uma famosa loja de comércio eletrônico tem um aparelho de TV à venda por R$ 1.000,00. Sabendo-se que a taxa de juros é 5% ao mês, pergunta-se: Qual será o valor da prestação se fizermos o pagamento em 3 vezes sem entrada?

Primeiramente veja que o termo sem entrada significa dizer que todos os mil reais serão financiados e por isto irão sofrer a incidência de juros. Se a primeira parcela fosse paga no momento da compra, o valor financiado seria a diferença entre os mil reais e o valor pago na entrada.

O valor da mercadoria sem os juros é chamado de valor presente, sendo identificado pela variável PV. Dito isto, temos que as variáveis do problema são:

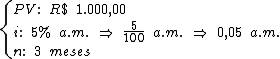
Primeiramente vamos ao cálculo do coeficiente de financiamento através da fórmula vista acima:

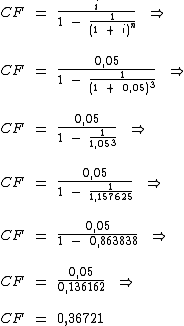
Sabendo-se que o coeficiente de financiamento é igual a 0,36721 e que o valor da prestação é identificado pela variável PMT, podemos utilizar a fórmula abaixo para calcularmos o valor das parcelas:

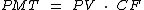
Calculando temos:

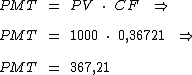
Ou seja:

O valor da prestação para o pagamento em 3 vezes sem entrada será de R$ 367,21.

Ao multiplicarmos o valor da prestação por três iremos obter o valor a prazo de R$ 1.101,63. O valor dos juros é, portanto de R$ 101,63.

Embora seja óbvio que o valor de R$ 367,21 relativo a cada uma das três parcelas deva pagar o valor do produto à vista e ainda cobrir os juros do período, vamos ainda assim conferir se a conta fecha. Vejamos a tabela abaixo:

Período	Valor a Pagar	Juros	Total a Pagar	Valor Pago	Saldo
1	R$ 1.000,00	R$ 50,00	R$ 1.050,00	R$ 367,21	R$ 682,79
2	R$ 682,79	R$ 34,14	R$ 716,93	R$ 367,21	R$ 349,72
3	R$ 349,72	R$ 17,49	R$ 367,21	R$ 367,21	R$ 0,00

Analisando a tabela verificamos que os juros embutidos nas prestações totalizam exatamente o valor calculado anteriormente de R$ 101,63, além disto como as três parcelas pagas totalizam R$ 1.101,63, ao descontarmos os juros pagos temos que a diferença de R$ 1.000,00 cobre exatamente o valor à vista do produto, comprovando que o coeficiente de financiamento nos permite calcular com exatidão o valor das prestações em operações envolvendo juros.

Agora veremos um exemplo de pagamento com entrada, sendo que o valor da entrada seja diferente do valor das prestações:

Agora nesta loja quero comprar um outro aparelho de TV à venda também por R$ 1.000,00. Sei que a taxa de juros ainda é 5% ao mês, pergunta-se: Qual será o valor da prestação se fizermos o pagamento em 3 vezes sendo que será que pago R$ 400,00 de entrada?

Agora como temos uma entrada de R$ 400,00, significa dizer que dos mil reais serão financiados apenas R$ 600,00 e por isto apenas eles irão sofrer a incidência de juros.

Devemos observar que agora o período de financiamento é de apenas dois meses e não mais três meses, já que o valor da entrada será dado no ato da compra, ficando então apenas duas prestações a serem pagas. O valor da entrada não foi financiado e por isto não incidirá juros sobre o mesmo.

As variáveis do problema são então:

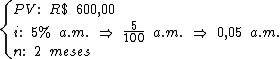
Vamos ao cálculo do coeficiente de financiamento:

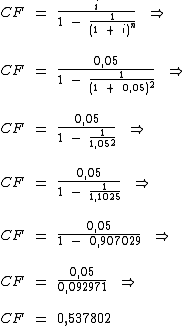
Agora utilizaremos a fórmula abaixo, a mesma utilizada anteriormente, para calcularmos o valor das parcelas:

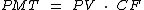
Ao calcularmos temos:

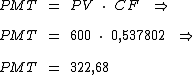
Concluindo:

O valor da prestação para o pagamento em 2 vezes com uma entrada no valor de R$ 400,00 será de R$ 322,68.

E se ao invés de dar uma entrada de R$ 400,00, eu quisesse que o valor da entrada fosse o mesmo valor das prestações? Vejamos mais este exemplo:

Ainda nesta loja na qual compro frequentemente, quero comprar mais um outro aparelho de TV à venda também por R$ 1.000,00. A taxa de juros também é 5% ao mês. Quero pagar ainda em 3 vezes sendo uma entrada e mais duas parcelas iguais ao valor da entrada. Qual o valor da entrada e consequentemente o valor das prestações?

Para o cálculo do coeficiente de financiamento temos as variáveis:

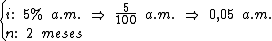
O número de parcelas é igual a dois, pois a entrada é paga no ato da compra e, portanto não é financiada. Sempre que tivermos um valor de entrada, o número de parcelas será abatido em uma unidade, já que o primeiro pagamento será realizado no ato da aquisição.

Note que em relação ao exemplo anterior, nem i, nem n foram alteradas, então o coeficiente de financiamento será o mesmo calculado anteriormente:

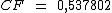
Sabemos que a fórmula para o cálculo das prestações é a seguinte:

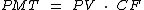
Só que neste caso PV deve ser abatido no mesmo valor da prestação. Então a fórmula ficaria:

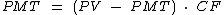
Vamos então passo a passo isolar à esquerda a variável PMT:

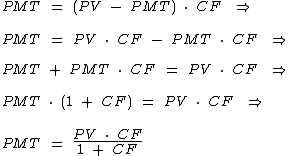
Temos então uma nova fórmula para o cálculo do valor de prestações com o mesmo valor da entrada:

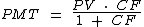
O valor da variável PV é o valor à vista da mercadoria. Logo PV = 1000.

Vamos aos cálculos:

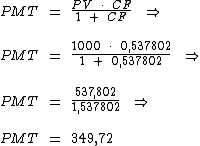
Portanto:

O valor da entrada e das prestações será de R$ 349,72.

Vejamos agora um exemplo de a partir do valor final com juros, chegarmos ao valor à vista:

Aquela famosa loja de comércio eletrônico tem um outro aparelho de TV à venda pelo valor total R$ 3.174,12 se pago em 12 vezes à taxa de juros é 1,99% ao mês. Qual é o valor desta TV à vista?

Ao dividirmos o valor total a prazo de R$ 3.174,12 por 12 que é o número de parcelas obteremos R$ 264,51 que corresponde ao valor de cada prestação.

Logo mais acima vimos que a fórmula seguinte é utilizada para calcularmos o valor das prestações se tivermos o valor à vista e o coeficiente de financiamento:

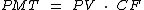
Como o que nos interessa agora é obter o valor presente, vamos isolá-lo na expressão acima:

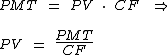
O cálculo do coeficiente de financiamento utilizará as seguintes variáveis:

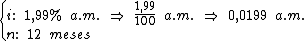
Então vamos calculá-lo:

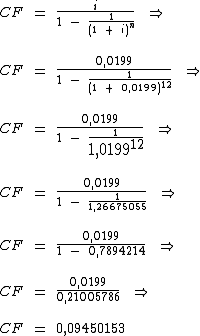
Finalmente podemos então calcular o valor à vista da TV:

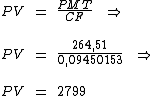
Portanto:

O valor à vista desta TV é de R$ 2.799,00.