Exercícios resolvidos - Juros simples - Parte 3
Para maiores informações teóricas sobre este assunto veja também:Teoria - Juros simples
41) Calcule o montante e os juros referentes a um capital de
R$ 186.500,00 investido a 6,5% a.b., durante 4 trimestres.
Veja que neste caso a taxa de juros e o período não estão na mesma unidade de
tempo. Neste caso, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
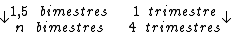
Resolvendo:
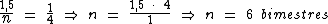
Identificando-se os termos disponíveis, temos:
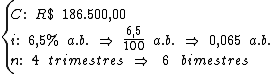
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
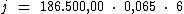
Logo:
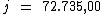
O montante é obtido somando-se ao valor do capital, o valor total dos juros.
Tal como na fórmula:
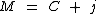
Ao substituirmos o valor dos termos temos:
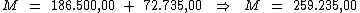
Portanto:
Ao aplicarmos um capital de R$ 186.500,00 investido a 6,5% a.b.,
durante 4 trimestres, obteremos um juro total de R$ 72.735,00 e um
montante de R$ 259.235,00.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
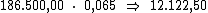
Ora, sendo o valor do juro em cada período correspondente a R$ 12.122,50,
resta-nos multiplicar este valor por 6, correspondente ao período de tempo,
para termos o valor procurado:
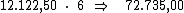
O valor do montante será encontrado, simplesmente somando-se ao valor do
principal, o valor total dos juros:
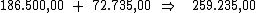
42) Beltrano tomou emprestado R$ 350.000,00 durante 2 semestres,
à taxa de juros simples de 45% a.a. Qual o juro resultante após os
2 semestres?
Observe que neste caso a taxa de juros e o período não estão na mesma unidade
de tempo. Nestas condições, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
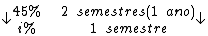
Resolvendo:
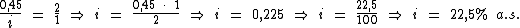
Identificando-se as variáveis disponíveis, temos:
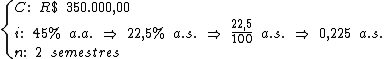
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
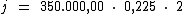
Logo:
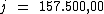
Portanto:
Ao tomar emprestado R$ 350.000,00 à taxa de juros simples de
45% a.a., por 2 semestres Beltrano pagará de juros um total de
R$ 157.500,00.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
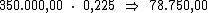
Ora, sendo o valor do juro em cada período correspondente a R$ 78.750,00,
resta-nos multiplicar este valor por 2, correspondente ao período de tempo,
para termos o valor procurado:
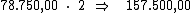
43) Para comprar uns utensílios domésticos, uma pessoa realizou um
empréstimo a uma taxa de juros simples de 5,4% a.m. Sabe-se que a duração
do empréstimo foi de 5 meses, qual o juro pago para um empréstimo de
R$ 500,00?
Identificando-se os termos disponíveis, temos:
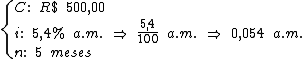
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
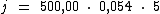
Logo:
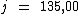
Portanto:
O capital de R$ 500,00 emprestado a 5,4% a.m., durante 5 meses
resultou em um juro total de R$ 135,00.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
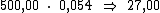
Ora, sendo o valor do juro em cada período correspondente a R$ 27,00,
resta-nos multiplicar este valor por 5, correspondente ao período de tempo,
para termos o valor procurado:
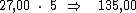
44) Qual o valor dos juros e do montante resultantes de um empréstimo de
R$ 54.100,00 feito pelo prazo de 4 anos, à taxa de 19,5% a.a.?
Identificando-se as variáveis disponíveis, temos:
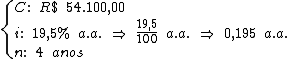
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
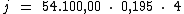
Logo:
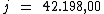
O montante é obtido somando-se ao valor do capital, o valor total dos juros.
Tal como na fórmula:
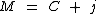
Ao substituirmos o valor das variáveis temos:
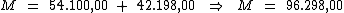
Portanto:
O valor dos juros será de R$ 42.198,00, resultante do empréstimo de
R$ 54.100,00 à taxa de 19,5% a.a., pelo prazo de 4 anos. O
montante será de R$ 96.298,00.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
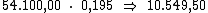
Ora, sendo o valor do juro em cada período correspondente a R$ 10.549,50,
resta-nos multiplicar este valor por 4, correspondente ao período de tempo,
para termos o valor procurado:
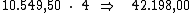
O valor do montante será encontrado, simplesmente somando-se ao valor do
principal, o valor total dos juros:
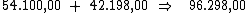
45) Qual o valor dos juros correspondente a um empréstimo de
R$ 62.200,00 realizado pelo prazo de 5 bimestres, à taxa de
21,3% a.t.?
Veja que neste caso a taxa de juros e o período não estão na mesma unidade de
tempo. Neste caso, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
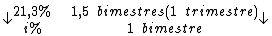
Resolvendo:
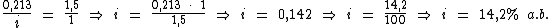
Identificando-se os termos disponíveis, temos:
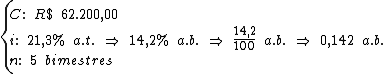
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
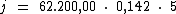
Logo:
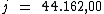
Portanto:
O valor dos juros será de R$ 44.162,00, correspondente ao empréstimo de
R$ 62.200,00 à taxa de 21,3% a.t., pelo prazo de 5 bimestres.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
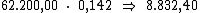
Ora, sendo o valor do juro em cada período correspondente a R$ 8.832,40,
resta-nos multiplicar este valor por 5, correspondente ao período de tempo,
para termos o valor procurado:
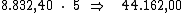
46) Comprei uma casa pagando um total de R$ 149.838,00, sendo que
paguei R$ 34.578,00 de juros, a uma taxa de 2% a.m., por quantos
meses eu financiei esta casa? Qual o preço dela sem os juros?
Primeiramente iremos calcular o valor do capital.
A diferença entre o montante (R$ 149.838,00) e o valor total do juro
(R$ 34.578,00), nos dá o valor do capital:
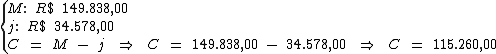
Identificando-se as variáveis disponíveis, temos:
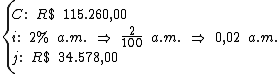
Para calcularmos o período de tempo utilizaremos a fórmula:
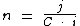
Substituindo o valor dos termos temos:
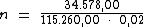
Logo:
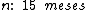
Portanto:
O preço da casa sem os juros foi de R$ 115.260,00 e o prazo de
financiamento foi de 15 meses.
Sem utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, pelo seguinte
raciocínio:
Ao multiplicarmos o valor do capital pela taxa de juros, iremos obter o juro
referente a cada período:
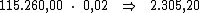
Neste caso, basta-nos dividir o valor de R$ 34.578,00, referente ao valor
total do juro, por R$ 2.305,20 correspondente ao valor do juro em cada
período, obtendo assim o período de tempo procurado:
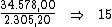
47) Jandira comprou seu carro pagando um total de R$ 38.792,00, o
valor do capital é de R$ 20.000,00 e a taxa de juros é de 2,61% a.m.
Qual o prazo desta aplicação em semestres?
Em primeiro lugar, devemos calcular o valor do juro total.
Obtemos o valor do juro total ao subtrairmos do montante
(R$ 38.792,00), o valor do capital (R$ 20.000,00):
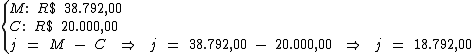
Veja bem que neste caso a taxa de juros e o período não estão na mesma unidade
de tempo. Sendo assim, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
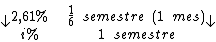
Resolvendo:
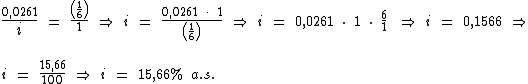
Identificando-se os termos disponíveis, temos:
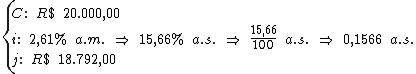
Para calcularmos o período de tempo utilizaremos a fórmula:
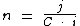
Substituindo o valor dos termos temos:
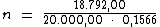
Logo:
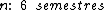
Portanto:
O prazo de pagamento do carro de Jandira foi de 6 semestres.
Sem utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, pelo seguinte
raciocínio:
Ao multiplicarmos o valor do capital pela taxa de juros, iremos obter o juro
referente a cada período:
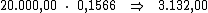
Desta forma, basta-nos dividir o valor de R$ 18.792,00, referente ao valor
total do juro, por R$ 3.132,00 correspondente ao valor do juro em cada
período, obtendo assim o período de tempo procurado:
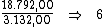
48) O montante de uma aplicação realizada por Fulano é R$ 161.829,92,
o valor dos juros de R$ 110.617,92 decorridos 8 meses, qual a taxa de
juros a.d.?
Inicialmente o valor do capital será obtido subtraindo-se do montante
(R$ 161.829,92), o valor total do juro (R$ 110.617,92):
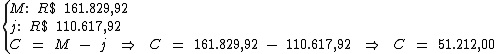
Esteja atento que neste caso a taxa de juros e o período não estão na mesma
unidade de tempo. Quando isto acontece, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
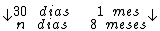
Resolvendo:
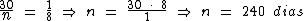
Identificando-se as variáveis disponíveis, temos:
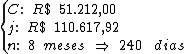
Para calcularmos a taxa de juros utilizaremos a fórmula:
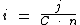
Substituindo o valor dos termos temos:
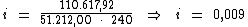
Logo:
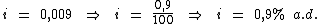
Portanto:
A taxa de juros da aplicação realizada por Fulano é de 0,9% a.d.
Alternativamente poderíamos dividir o valor total dos juros,
R$ 110.617,92, pelo valor do principal, R$ 51.212,00, de sorte a
encontrar a taxa de juros total do período:
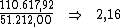
Dividindo-se então, esta taxa de 2,16 pelo período de tempo, 240, obteríamos a
taxa desejada:
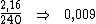
49) O valor principal duma aplicação é de R$ 36.000,00, o qual gerou
um montante de R$ 55.440,00 em 4,5 anos. Qual o valor dos juros e a
sua respectiva taxa a.b.?
Para começar, devemos calcular o valor do juro total subtraindo-se do montante
(R$ 55.440,00), o valor do capital (R$ 36.000,00):
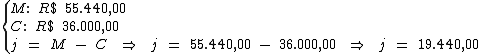
Veja que neste caso a taxa de juros e o período não estão na mesma unidade de
tempo. Neste caso, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
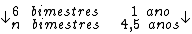
Resolvendo:
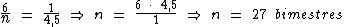
Identificando-se os termos disponíveis, temos:
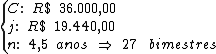
Para calcularmos a taxa de juros utilizaremos a fórmula:
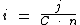
Substituindo o valor dos termos temos:
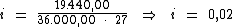
Logo:
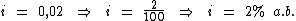
Portanto:
A taxa de juros desta aplicação é de 2% a.b. O valor dos juros é de
R$ 19.440,00.
Alternativamente poderíamos dividir o valor total dos juros, R$ 19.440,00,
pelo valor do principal, R$ 36.000,00, de forma a encontrar a taxa de
juros total do período:
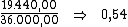
Dividindo-se então, esta taxa de 0,54 pelo período de tempo, 27, obteríamos a
taxa desejada:
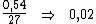
50) Margarida comprou uma geladeira que custa R$ 2.550,00, a uma taxa
de juros simples de 1,8% a.m. pelo período de 2 anos, qual o valor
total a pagar? Qual o valor dos juros?
Observe que neste caso a taxa de juros e o período não estão na mesma unidade
de tempo. Nestas condições, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
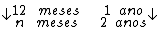
Resolvendo:
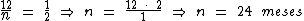
Identificando-se as variáveis disponíveis, temos:
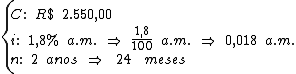
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
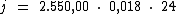
Logo:
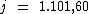
O montante é obtido somando-se ao valor do capital, o valor total dos juros.
Tal como na fórmula:
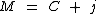
Ao substituirmos o valor das variáveis temos:
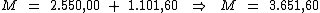
Portanto:
O valor dos juros será de R$ 1.101,60, que acrescentado ao preço da
geladeira de R$ 2.550,00, irá totalizar R$ 3.651,60.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
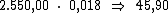
Ora, sendo o valor do juro em cada período correspondente a R$ 45,90,
resta-nos multiplicar este valor por 24, correspondente ao período de tempo,
para termos o valor procurado:
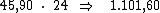
O valor do montante será encontrado, simplesmente somando-se ao valor do
principal, o valor total dos juros:
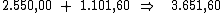
51) Ciclano e Fulana investiram R$ 70.000,00 por 4 semestres, à
taxa de juros simples de 30% a.a., para realizarem os preparativos de seu
casamento. Quanto ganharam com o investimento?
Veja bem que neste caso a taxa de juros e o período não estão na mesma unidade
de tempo. Sendo assim, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
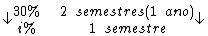
Resolvendo:
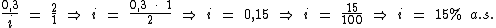
Identificando-se os termos disponíveis, temos:
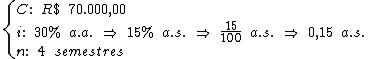
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
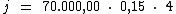
Logo:
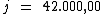
Portanto:
Com investimento ganharam um juros total de R$ 42.000,00.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
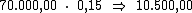
Ora, sendo o valor do juro em cada período correspondente a R$ 10.500,00,
resta-nos multiplicar este valor por 4, correspondente ao período de tempo,
para termos o valor procurado:
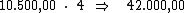
52) Saquei os R$ 7.000,00 de juros que minha aplicação rendeu. O
dinheiro ficou investido por 14 meses. Eu havia aplicado
R$ 31.250,00. Qual foi a taxa de juros a.a. da aplicação?
Identificando-se as variáveis disponíveis, temos:
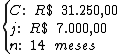
Para calcularmos a taxa de juros utilizaremos a fórmula:
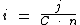
Substituindo o valor dos termos temos:
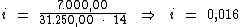
No entanto, como a unidade de tempo da taxa solicitada está em anos ('a.a.') e
o cálculo foi realizado na unidade do período de tempo que está em 'meses',
devemos converter a unidade de tempo da taxa calculada de a.m. ('meses') para
a.a. ('anos').
Logo:
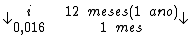
Resolvendo:
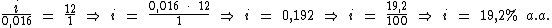
Portanto:
A taxa de juros simples da aplicação foi de 19,2% a.a.
Alternativamente poderíamos dividir o valor total dos juros, R$ 7.000,00,
pelo valor do principal, R$ 31.250,00, de forma a encontrar a taxa de
juros total do período:
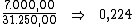
Dividindo-se então, esta taxa de 0,224 pelo período de tempo, 14, obteríamos a
taxa desejada:
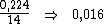
Resta ainda converter a taxa de juros para a unidade de tempo solicitada, o que
pode ser feito se realizando o procedimento de conversão conforme efetuado
acima.
53) Meu vizinho realizou uma aplicação por um período de 1 semestre.
Em tal período o principal de R$ 4.650,00 rendeu a ele R$ 2.790,00 de
juros. Qual foi a taxa de juros a.m. utilizada?
Veja que neste caso a taxa de juros e o período não estão na mesma unidade de
tempo. Neste caso, devemos converter uma das unidades.
Identificando-se os termos disponíveis, temos:
Para calcularmos a taxa de juros utilizaremos a fórmula:
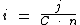
Substituindo o valor dos termos temos:
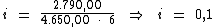
Logo:
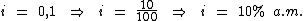
Portanto:
A aplicação foi realizada à uma taxa de juros simples de 10% a.m.
Alternativamente poderíamos dividir o valor total dos juros, R$ 2.790,00,
pelo valor do principal, R$ 4.650,00, de maneira a encontrar a taxa de
juros total do período:
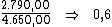
Dividindo-se então, esta taxa de 0,6 pelo período de tempo, 6, obteríamos a
taxa desejada:
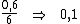
54) Felipe recebeu R$ 2.200,00 de juros, por um empréstimo de
90 dias. A taxa de juros aplicada foi de 5,4% a.a. Quanto Felipe
havia emprestado?
Observe que neste caso a taxa de juros e o período não estão na mesma unidade
de tempo. Nestas condições, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
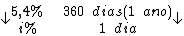
Resolvendo:
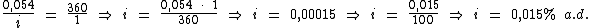
Identificando-se as variáveis disponíveis, temos:
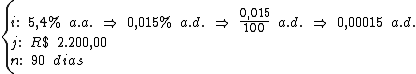
Para calcularmos o capital vamos utilizar a fórmula:
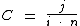
Substituindo o valor dos termos temos:
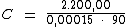
Logo:
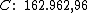
Portanto:
Felipe havia emprestado R$ 162.962,96, pelo qual recebeu R$ 2.200,00
de juros, à taxa de 5,4% a.a. pelo período de 90 dias.
Poderíamos chegar à mesma conclusão pela seguinte forma:
Se dividirmos o valor total dos juros pelo período de tempo, iremos obter o
valor do juro por período:
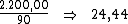
Portanto, ao dividirmos o valor do juro por período, R$ 24,44, pela taxa
de juros de 0,015%, iremos obter o valor do capital:
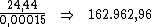
55) Marina recebeu R$ 11.137,00 de juros ao aplicar R$ 43.000,00
à taxa de 22,2% a.a. Qual foi o prazo da aplicação em meses?
Veja bem que neste caso a taxa de juros e o período não estão na mesma unidade
de tempo. Sendo assim, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
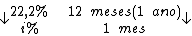
Resolvendo:
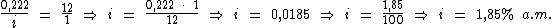
Identificando-se os termos disponíveis, temos:
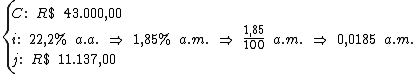
Para calcularmos o período de tempo utilizaremos a fórmula:
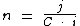
Substituindo o valor dos termos temos:
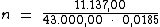
Logo:
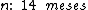
Portanto:
O prazo da aplicação foi de 14 meses. Aplicação esta que rendeu a Marina
R$ 11.137,00 de juros ao investir R$ 43.000,00 à taxa de
22,2% a.a.
Sem utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, pelo seguinte
raciocínio:
Ao multiplicarmos o valor do capital pela taxa de juros, iremos obter o juro
referente a cada período:
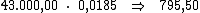
Neste caso, basta-nos dividir o valor de R$ 11.137,00, referente ao valor
total do juro, por R$ 795,50 correspondente ao valor do juro em cada
período, obtendo assim o período de tempo procurado:
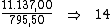
56) Calcule o montante e os juros referentes a um capital de
R$ 158.600,00 investido a 4,37% a.m., durante 15 bimestres.
Esteja atento que neste caso a taxa de juros e o período não estão na mesma
unidade de tempo. Quando isto acontece, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
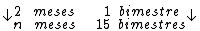
Resolvendo:
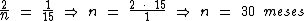
Identificando-se as variáveis disponíveis, temos:
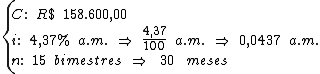
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
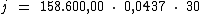
Logo:
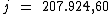
O montante é obtido somando-se ao valor do capital, o valor total dos juros.
Tal como na fórmula:
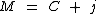
Ao substituirmos o valor das variáveis temos:
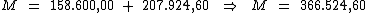
Portanto:
Ao aplicarmos um capital de R$ 158.600,00 investido a 4,37% a.m.,
durante 15 bimestres, obteremos um juro total de R$ 207.924,60 e um
montante de R$ 366.524,60.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
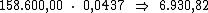
Ora, sendo o valor do juro em cada período correspondente a R$ 6.930,82,
resta-nos multiplicar este valor por 30, correspondente ao período de tempo,
para termos o valor procurado:
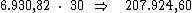
O valor do montante será encontrado, simplesmente somando-se ao valor do
principal, o valor total dos juros:
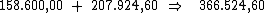
57) Fulano tomou emprestado R$ 500.000,00 durante 3 trimestres,
à taxa de juros simples de 15% a.s. Qual o juro resultante após os
3 trimestres?
Veja que neste caso a taxa de juros e o período não estão na mesma unidade de
tempo. Neste caso, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
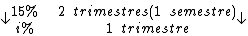
Resolvendo:
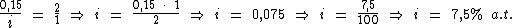
Identificando-se os termos disponíveis, temos:
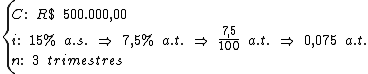
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
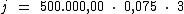
Logo:
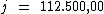
Portanto:
Ao tomar emprestado R$ 500.000,00 à taxa de juros simples de
15% a.s., por 3 trimestres Fulano pagará de juros um total de
R$ 112.500,00.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
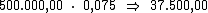
Ora, sendo o valor do juro em cada período correspondente a R$ 37.500,00,
resta-nos multiplicar este valor por 3, correspondente ao período de tempo,
para termos o valor procurado:
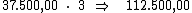
58) Para comprar um certo bem, uma pessoa realizou um empréstimo a uma
taxa de juros simples de 0,04% a.d. Sabe-se que a duração do empréstimo
foi de 15 meses, qual o juro pago para um empréstimo de R$ 17.500,00?
Observe que neste caso a taxa de juros e o período não estão na mesma unidade
de tempo. Nestas condições, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
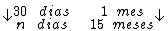
Resolvendo:
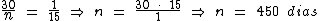
Identificando-se as variáveis disponíveis, temos:
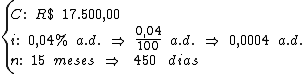
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
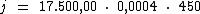
Logo:
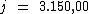
Portanto:
O capital de R$ 17.500,00 emprestado a 0,04% a.d., durante
15 meses resultou em um juro total de R$ 3.150,00.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
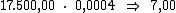
Ora, sendo o valor do juro em cada período correspondente a R$ 7,00,
resta-nos multiplicar este valor por 450, correspondente ao período de tempo,
para termos o valor procurado:
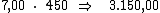
59) Qual o valor dos juros e do montante resultantes de um empréstimo de
R$ 45.100,00 feito pelo prazo de 6 anos, à taxa de 39% a.a.?
Identificando-se os termos disponíveis, temos:
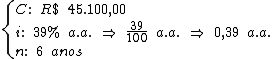
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
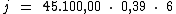
Logo:
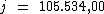
O montante é obtido somando-se ao valor do capital, o valor total dos juros.
Tal como na fórmula:
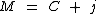
Ao substituirmos o valor dos termos temos:
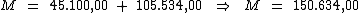
Portanto:
O valor dos juros será de R$ 105.534,00, resultante do empréstimo de
R$ 45.100,00 à taxa de 39% a.a., pelo prazo de 6 anos. O
montante será de R$ 150.634,00.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
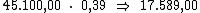
Ora, sendo o valor do juro em cada período correspondente a R$ 17.589,00,
resta-nos multiplicar este valor por 6, correspondente ao período de tempo,
para termos o valor procurado:
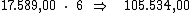
O valor do montante será encontrado, simplesmente somando-se ao valor do
principal, o valor total dos juros:
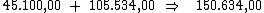
60) Qual o valor dos juros correspondente a um empréstimo de
R$ 26.000,00 realizado pelo prazo de 2 trimestres, à taxa de
14,2% a.s.?
Esteja atento que neste caso a taxa de juros e o período não estão na mesma
unidade de tempo. Quando isto acontece, devemos converter uma das unidades.
Montando uma regra de três simples direta, temos:
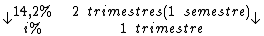
Resolvendo:
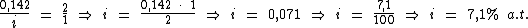
Identificando-se as variáveis disponíveis, temos:
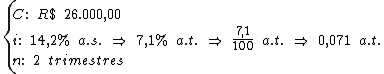
Para calcularmos o juro utilizaremos a fórmula:
Substituindo o valor dos termos temos:
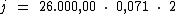
Logo:
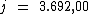
Portanto:
O valor dos juros será de R$ 3.692,00, correspondente ao empréstimo de
R$ 26.000,00 à taxa de 14,2% a.s., pelo prazo de 2 trimestres.
Ao invés de utilizarmos fórmulas, poderíamos chegar ao mesmo resultado, apenas
pela aplicação de alguns conceitos.
Como sabemos, o juro referente a cada período é calculado multiplicando-se o
valor do capital pela taxa de juros. Então o valor do juro por período seria:
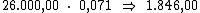
Ora, sendo o valor do juro em cada período correspondente a R$ 1.846,00,
resta-nos multiplicar este valor por 2, correspondente ao período de tempo,
para termos o valor procurado:
