Exercícios resolvidos - Divisão em Partes Proporcionais
Para maiores informações teóricas sobre este assunto veja também:Teoria - Divisão em partes diretamente proporcionais
1) Divida o número 51 em partes diretamente proporcionais a 2, 3, 5 e 7.
Sabemos que:
- p1 = K . 2
- p2 = K . 3
- p3 = K . 5
- p4 = K . 7
- p1 + p2 + p3 + p4 = 51
Para encontrarmos o valor da constante K devemos substituir o valor de p1, p2, p3 e p4 na última igualdade:
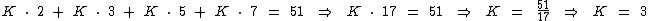
Logo:
- p1 = 3 . 2 = 6
- p2 = 3 . 3 = 9
- p3 = 3 . 5 = 15
- p4 = 3 . 7 = 21
As partes procuradas são respectivamente 6, 9, 15 e 21.
2) Divida o número 124 em parcelas diretamente proporcionais a 11, 7 e 13.
A partir do enunciado temos que:
- p1 = K . 11
- p2 = K . 7
- p3 = K . 13
- p1 + p2 + p3 = 124
Para encontrarmos o valor da constante K devemos substituir o valor de p1, p2 e p3 na última expressão:
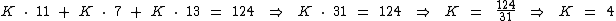
Portanto:
- p1 = 4 . 11 = 44
- p2 = 4 . 7 = 28
- p3 = 4 . 13 = 52
As parcelas procuradas são respectivamente 44, 28 e 52.
3) Divida o número 115 em partes inversamente proporcionais a 8, 3, 7 e 12.
Conforme o explicado na parte teórica sabemos que:
- p1 = K . 1/8
- p2 = K . 1/3
- p3 = K . 1/7
- p4 = K . 1/12
- p1 + p2 + p3 + p4 = 115
Para encontrarmos o valor da constante K devemos substituir o valor de p1, p2, p3 e p4 na última igualdade:
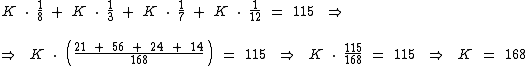
Logo:
- p1 = 168 . 1/8 = 21
- p2 = 168 . 1/3 = 56
- p3 = 168 . 1/7 = 24
- p4 = 168 . 1/12 = 14
As partes procuradas são respectivamente 21, 56, 24 e 14.
4) Divida o número 662 em parcelas inversamente proporcionais a 14, 27 e 15.
Do enunciado tiramos que:
- p1 = K . 1/14
- p2 = K . 1/27
- p3 = K . 1/15
- p1 + p2 + p3 = 662
Para encontrarmos o valor da constante K devemos substituir o valor de p1, p2 e p3 na última expressão:
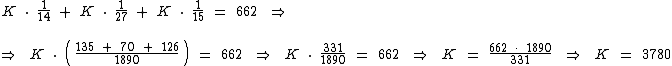
Portanto:
- p1 = 3780 . 1/14 = 270
- p2 = 3780 . 1/27 = 140
- p3 = 3780 . 1/15 = 252
As parcelas procuradas são respectivamente 270, 140 e 252.
5) Divida o número 600 em partes diretamente proporcionais a 12, 4, 2 e 6 e inversamente proporcionais a 6, 2, 3 e 18, respectivamente.
Conforme o enunciado sabemos que:
- p1 = K . 12/6
- p2 = K . 4/2
- p3 = K . 2/3
- p4 = K . 6/18
- p1 + p2 + p3 + p4 = 600
Para encontrarmos o valor da constante K devemos substituir o valor de p1, p2, p3 e p4 na última igualdade:
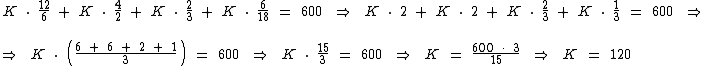
Logo:
- p1 = 120 . 12/6 = 240
- p2 = 120 . 4/2 = 240
- p3 = 120 . 2/3 = 80
- p4 = 120 . 6/18 = 40
As partes procuradas são respectivamente 240, 240, 80 e 40.
6) Divida o número 579 em partes diretamente proporcionais a 7, 4 e 8 e inversamente proporcionais a 2, 3 e 5, respectivamente.
A partir do enunciado temos:
- p1 = K . 7/2
- p2 = K . 4/3
- p3 = K . 8/5
- p1 + p2 + p3 = 579
Para encontrarmos o valor da constante K devemos substituir o valor de p1, p2 e p3 na última expressão:
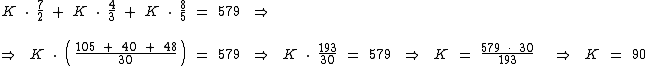
Portanto:
- p1 = 90 . 7/2 = 315
- p2 = 90 . 4/3 = 120
- p3 = 90 . 8/5 = 144
As parcelas procuradas são respectivamente 315, 120 e 144.
7) Três trabalhadores devem dividir R$ 1.200,00 referentes ao pagamento por um serviço realizado. Eles trabalharam 2, 3 e 5 dias respectivamente e devem receber uma quantia diretamente proporcional ao número de dias trabalhados. Quanto deverá receber cada um?
Conforme o enunciado deduzimos que:
- p1 = K . 2
- p2 = K . 3
- p3 = K . 5
- p1 + p2 + p3 = 1200
Para encontrarmos o valor da constante K devemos substituir o valor de p1, p2 e p3 na última expressão:
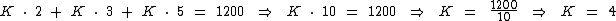
Portanto:
- p1 = 120 . 2 = 240
- p2 = 120 . 3 = 360
- p3 = 120 . 5 = 600
Quem trabalhou 2 dias irá receber R$ 240,00. R$ 360,00 será destinado ao que trabalhou 3 dias e ao terceiro caberá um pagamento de R$ 600,00.
8) Dois ambulantes obtiveram R$ 1.560,00 pela venda de certas mercadorias. Esta quantia deve ser dividida entre eles em partes diretamente proporcionais a 5 e 7, respectivamente. Quanto irá receber cada um?
Do enunciado temos que:
- p1 = K . 5
- p2 = K . 7
- p1 + p2 = 1560
Para encontrarmos o valor da constante K devemos substituir o valor de p1 e p2 na última expressão:
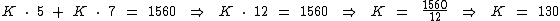
Portanto:
- p1 = 130 . 5 = 650
- p2 = 130 . 7 = 910
Os ambulantes iram receber respectivamente R$ 650,00 e R$ 910,00.
9) Os três jogadores mais disciplinados de um campeonato de futebol amador irão receber um prêmio de R$ 3.340,00 rateados em partes inversamente proporcionais ao número de faltas cometidas em todo o campeonato. Os jogadores cometeram 5, 7 e 11 faltas. Qual a premiação referente a cada um deles respectivamente?
Do enunciado tiramos que:
- p1 = K . 1/5
- p2 = K . 1/7
- p3 = K . 1/11
- p1 + p2 + p3 = 3340
Para encontrarmos o valor da constante K devemos substituir o valor de p1, p2 e p3 na última expressão:
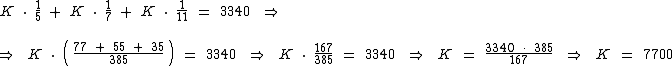
Portanto:
- p1 = 7700 . 1/5 = 1540
- p2 = 7700 . 1/7 = 1100
- p3 = 7700 . 1/11 = 700
A premiação será respectivamente R$ 1.540,00, R$ 1.100,00 e R$ 700,00.
10) Um pai distribuiu 546 bolas de gude aos seus 2 filhos em partes diretamente proporcionais à média final na disciplina de matemática e em partes inversamente proporcionais ao número de faltas em todo o ano letivo. O primeiro filho teve média final 9 e faltou 8 vezes, enquanto que o segundo filho teve média final 8 e faltou 3 vezes. Quantas bolas de gude eles ganharam respectivamente?
Como sabemos, a partir do enunciado podemos montar as seguintes igualdades:
- p1 = K . 9/8
- p2 = K . 8/3
- p1 + p2 = 546
Para encontrarmos o valor da constante K devemos substituir o valor de p1 e p2 na última expressão:
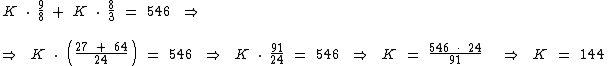
Portanto:
- p1 = 144 . 9/8 = 162
- p2 = 144 . 8/3 = 384
O primeiro filho ganhou 162 bolas de gude e o segundo ganhou 384.
