Progressão Geométrica
Uma sucessão de números na qual o quociente entre dois termos consecutivos é constante, é denominada progressão geométrica, ou abreviadamente de P.G.
Representação de uma P.G.
Representando por a1 o primeiro elemento, por a2 o segundo elemento de uma P.G. e assim sucessivamente, até o último elemento que é representado por an, temos a seguinte representação para uma progressão geométrica:
P.G. ( a1, a2, a3, a4, ..., an ).
A representação acima se refere a uma P.G. finita com n elementos. Caso a sucessão seja infinita, utilizamos a seguinte representação:
P.G. ( a1, a2, a3, a4, ..., an, ... ).
Terminologia
P.G. ( 3, 12, 48, 192, 768 )
Acima temos a representação de uma progressão geométrica finita.
Um termo qualquer é identificado por an, onde n indica a posição deste termo. Por exemplo, o termo a3 se refere ao terceiro termo desta P.G., que no caso é igual a 48, já o primeiro termo, a1, nesta P.G. é igual a 3.
Como citado acima, o quociente entre dois termos consecutivos de uma P.G. é constante. Neste exemplo este valor é igual a 4, por exemplo, a divisão do segundo pelo primeiro termo é igual a 4.
Este valor constante que é o quociente entre um termo e outro é denominado razão da progressão geométrica e é representado pela letra q.
Se representamos um termo qualquer de uma P.G. por an, então podemos dizer que o seu antecedente é igual a an - 1 e que o seu consequente é igual a an + 1.
Desta forma podemos dizer que 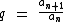 , ou ainda
, ou ainda 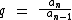 .
.
Veja estes exemplos: 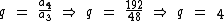 e também
e também 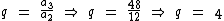 .
.
Além disto temos que um termo qualquer de uma P.G. é média geométrica entre o seu antecedente e o seu consequente:
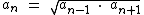
Progressão geométrica constante
Uma progressão geométrica é constante quando a sua razão é igual a 1, ou quando o primeiro termo é igual a zero. Neste caso todos os termos da P.G. têm o mesmo valor.
Exemplos:
P.G. ( 0, 0, 0, 0, ... )
P.G. ( 5, 5, ..., 5 )
P.G. ( 9, 9, 9 )
No primeiro exemplo temos que a1 = 0 e nos outros dois q = 1.
Progressão geométrica crescente
Uma progressão geométrica é crescente quando o consequente de um termo qualquer é maior que este termo. Isto ocorre quando q > 1 e a1 > 0, ou quando 0 < q < 1 e a1 < 0.
Exemplos:
P.G. ( 1, 2, 4, ... )
P.G. ( -480, -120, -30, ... )
Note que a razão das progressões acima é respectivamente 2 e 0,25. No primeiro caso, q > 1 e a1 > 0 e no segundo caso temos que 0 < q < 1 e a1 < 0.
Progressão geométrica decrescente
Uma progressão geométrica é decrescente quando o consequente de um termo qualquer é menor que este termo. Isto ocorre quando q > 1 e a1 < 0, ou quando 0 < q < 1 e a1 > 0.
Exemplos:
P.G. ( -35, -105, -315, ... )
P.G. ( 1400, 560, 224, ... )
Veja que a razão das progressões acima é respectivamente 3 e 0,4. No primeiro exemplo, q > 1 e a1 < 0 e no segundo temos que 0 < q < 1 e a1 > 0.
Progressão geométrica alternante ou oscilante
Uma progressão geométrica cujos termos alternem ou oscilem de positivo para negativo e vice-versa, é denominada P.G. oscilante ou P.G. alternante. Isto ocorre quando q < 0 e a1 ≠ 0.
Exemplos:
P.G. ( -3, 6, -12, ... )
P.G. ( 729, -218,7, 65,61, -19,683, ... )
Em ambos os casos a1 ≠ 0. No primeiro caso a razão é igual a -2, logo q < 0 e no segundo temos que a razão é igual a -0,3, portanto também temos q < 0.
Fórmula do termo geral de uma P.G.
Sabemos que o termo seguinte a um termo de uma P.G. é igual ao referido termo multiplicado pela razão q. Para uma P.G. genérica podemos dizer que o segundo termo é igual ao primeiro termo, a1, vezes a razão q:
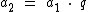
O terceiro termo é resultado da multiplicação do segundo termo pela razão:
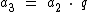
No entanto como vimos que a2 = a1 . q, substituindo-o na expressão temos:
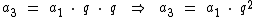
O quarto termo é resultado do produto do terceiro termo com a razão e como sabemos que a3 = a1 . q2, temos:
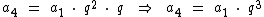
Pelo mesmo raciocínio, o quinto termo será:
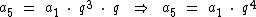
O sexto termo será:
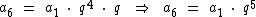
De forma resumida temos:
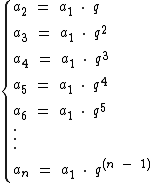
Portanto, partindo-se do primeiro termo, a fórmula do termo geral de uma progressão geométrica é:
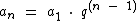
Mas e se partirmos de outro termo que não o primeiro?
Vejamos:
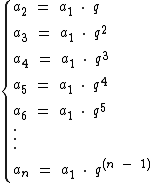
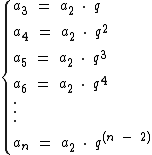
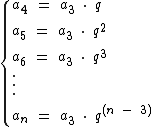
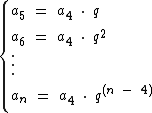
Na fórmula do termo geral da P.G., subtraímos 1 de n quando partimos do termo a1, perceba que quando partimos do termo a2, subtraímos 2 de n, assim como subtraímos 3 ao partirmos de a3 e 4 quando partirmos de a4. Partindo então de um termo m, podemos reescrever a fórmula do termo geral da P.G. como:
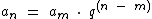
Compreendendo a fórmula do termo geral da P.G. em função de qualquer termo
Como já fizemos no caso da P.A., vamos a um exemplo para que a explicação fique de mais fácil entendimento.
Através da fórmula acima, vamos expressar o termo a7 de uma P.G. genérica, em função do termo a4:
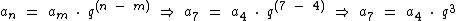
Temos então que o termo a7 pode ser expresso em função do termo a4 como:
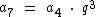
Agora preste bastante atenção ao seguinte:
Sabemos que o próximo termo após a4, é o termo a5, que equivale a a4 vezes q. Para chegarmos ao próximo termo, o a6, multiplicamos mais uma vez pela razão q e para chegarmos finalmente ao termo a7, multiplicamos mais outra vez por q, ou seja, como nos deslocamos três posições à direita, multiplicamos a4 por q3 para chegarmos ao termo a7. Veja que foi exatamente este o resultado obtido em função da fórmula, ou seja, a7 = a4 . q3.
Vejamos que este raciocínio é bem mais prático que recorrermos à formula, para voltarmos de a7 para a4:
Agora o termo procurado está à esquerda do termo atual, na verdade três posições à sua esquerda, então vamos multiplicar a7 por q-3, temos então que a4 = a7 . q-3, que equivale a dividirmos a7 por q três vezes.
Então vamos chegar ao mesmo resultado através da fórmula para confirmarmos esta explicação:
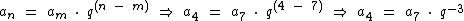
Resumindo, se partindo do termo atual iremos avançar n termos à direita, para chegarmos ao termo final, então temos que multiplicar o termo inicial por n vezes a razão q, ou seja, multiplicá-lo por qn. Se nos deslocarmos à esquerda, o procedimento é semelhante, só que ao invés de multiplicarmos, iremos dividir o termo inicial n vezes pela razão q, o que equivale a multiplicá-lo por q-n.
Como exemplo temos que a15 = a11 . q4, pois avançamos 4 termos de a11 a a15, assim como a2 = a7 . q-5, pois retrocedemos 5 termos de a7 para a2.
Soma dos termos de uma P.G.
Podemos expressar a soma dos n termos de uma P.G. finita como:
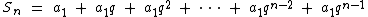
Multiplicando-a pela razão q temos:
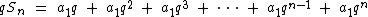
Vamos analisar o segundo membro das duas expressões. Note que o segundo termo da primeira expressão é igual ao primeiro termo da segunda expressão, a mesma coisa ocorre com o segundo, terceiro, quarto, até o último termo do segundo membro da primeira expressão.
Ao subtrairmos a primeira expressão da segunda, estes termos que ocorrem em duplicidade são anulados e ficamos então com a seguinte expressão:
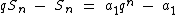
Temos então:
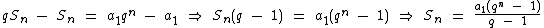
Portanto podemos utilizar a fórmula abaixo para calcularmos a soma de todos os termos de uma P.G. finita e também dos n primeiros termos de uma P.G. qualquer, desde que q ≠ 1:
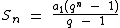
Para q = 1 temos uma fórmula mais simples:
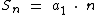
Produto dos termos de uma P.G.
Como feito no caso da soma, vamos agora deduzir a fórmula de cálculo do produto dos termos de uma progressão geométrica. Vejamos:
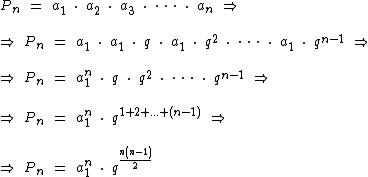
Portanto a fórmula para o cálculo do produto dos termos de uma P.G. finita, ou do produto dos n primeiros termos de uma P.G. é:
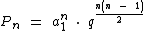
Exemplos de problemas envolvendo Progressão Geométrica
 Formamos uma P.G. partindo do número 5 e o multiplicando sucessivamente por 3, até finalizarmos no número 17.433.922.005. Quantos termos há nesta progressão geométrica?
Formamos uma P.G. partindo do número 5 e o multiplicando sucessivamente por 3, até finalizarmos no número 17.433.922.005. Quantos termos há nesta progressão geométrica?
Identificando as variáveis do problema temos:
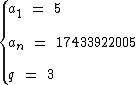
Através da aplicação da fórmula do termo geral iremos calcular o número de termos da progressão:
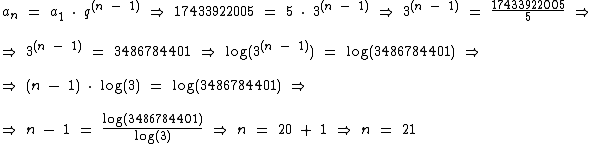
Portanto:
 Nesta progressão geométrica há 21 termos.
Nesta progressão geométrica há 21 termos.
 Qual é a soma dos termos da P.G. ( 8, 56, 392, ..., 134456)?
Qual é a soma dos termos da P.G. ( 8, 56, 392, ..., 134456)?
A partir do enunciado podemos calcular a razão da progressão:
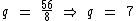
Para calcularmos a soma dos termos, primeiramente precisamos saber quantos eles são. Os dados disponíveis que temos para calcular esta quantidade são:
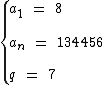
Calculando n temos:
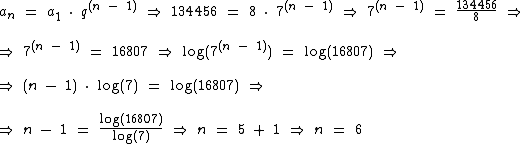
Agora que sabemos quantos termos são, podemos calcular a soma dos mesmos:
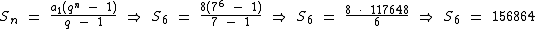
Logo:
 A soma dos termos da referida P.G. é igual a 156864.
A soma dos termos da referida P.G. é igual a 156864.






