Exercícios resolvidos - Progressão Geométrica
Para maiores informações teóricas sobre este assunto veja também:Progressão Geométrica
 1) Represente os termos a7, a2, a3 e a4, de uma P.G., em função dos a9, a5, a1 e a3 respectivamente.
1) Represente os termos a7, a2, a3 e a4, de uma P.G., em função dos a9, a5, a1 e a3 respectivamente.
Para que você consiga resolver com mais habilidade os próximos exercícios, é fundamental que você consiga entender perfeitamente o conceito aplicado na resolução deste exercício, portanto preste bastante atenção e o estude quantas vezes forem necessárias, até que o tenha compreendido por completo.
Na parte teórica deste tema vimos que a partir da fórmula do termo geral da P.G. em função de qualquer termo, exibida abaixo, podemos representar um termo específico em função de qualquer outro termo.
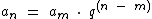
Para representarmos a7 em função de a9 temos:
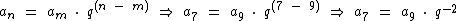
Entretanto vimos que na prática esta fórmula nada mais faz que determinar o número de termos de um ao outro e aplicar este número como o coeficiente de q, que irá multiplicar o termo original. Se o termo final estiver à direita (depois) do termo original o coeficiente será positivo, se estiver à esquerda (antes) será negativo.
a9 está dois termos à direita a7, logo precisamos dividi-lo duas vezes pela razão: a7 = a9 . q-2.
a5 vem três termos depois de a2, portanto precisamos dividi-lo três vezes pela razão: a2 = a5 . q-3.
a1 vem dois termos antes de a3, logo precisamos multiplicá-lo duas vezes pela razão: a3 = a1 . q2.
a3 está um termo à esquerda a4, portanto precisamos multiplicá-lo uma vez pela razão: a4 = a3 . q.
Então:
 a7 = a9 . q-2, a2 = a5 . q-3, a3 = a1 . q2 e a4 = a3 . q
a7 = a9 . q-2, a2 = a5 . q-3, a3 = a1 . q2 e a4 = a3 . q
 2) O produto dos 7 termos de uma P.G. é igual a 4586471424. Qual é o quarto termo?
2) O produto dos 7 termos de uma P.G. é igual a 4586471424. Qual é o quarto termo?
Se representarmos todos os termos desta progressão em função de a4 teremos:
P.G. ( a4q-3, a4q-2, a4q-1, a4, a4q, a4q2, a4q3 ).
A representação do produto dos termos será então:
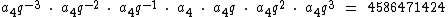
Perceba que na expressão acima q-3 anula q3, assim como q-2 anula q2 e q-1 anula q, deixando a mesma apenas com a variável a4. Isto ocorre apenas porque utilizamos o termo central como referência. Se tivéssemos escolhido qualquer outro termo, como o a3, por exemplo, para representarmos todos os outros termos em função dele, isto não iria ocorrer pois ele não é o termo central. Em função disto é fácil concluir que se a progressão tivesse um número par de termos, tal técnica não poderia ser utilizada.
Após esta breve explicação vamos continuar a resolução do exercício:
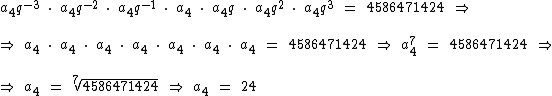
Portanto:
 O quarto termo é igual a 24.
O quarto termo é igual a 24.
 3) Dadas as sucessões P.G. ( x, y, 147 ) e P.A. ( 5x, y, 27 ), ambas crescentes, quais os valores de x e de y?
3) Dadas as sucessões P.G. ( x, y, 147 ) e P.A. ( 5x, y, 27 ), ambas crescentes, quais os valores de x e de y?
O termo y é média geométrica da P.G. e média aritmética da P.A., então matematicamente podemos igualar as duas médias assim:
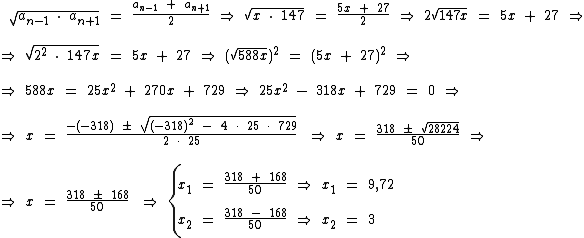
A variável x pode assumir, portanto os valores 3 e 9,72.
Para x = 9,72 temos a P.A. ( 48,6, y, 27 ) que não é aceitável pois o enunciado especifica uma P.A. crescente, então não podemos considerar o valor 9,72.
Para x = 3 temos a P.A. ( 15, y, 27 ) e a P.G. ( 3, y, 147 ) que estão dentro dos padrões do enunciado.
Como y é um termo médio, tanto da P.A., quanto da P.G., vamos calculá-lo na P.A., pois é mais simples:
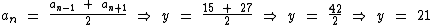
Assim sendo:
 O valor de x é 3 e o valor de y é 21.
O valor de x é 3 e o valor de y é 21.
 4) O sexto termo de uma P.G. é igual a 12500. Se a razão é igual a 5, qual é o terceiro termo?
4) O sexto termo de uma P.G. é igual a 12500. Se a razão é igual a 5, qual é o terceiro termo?
Como o terceiro termo está 3 termos à esquerda do sexto termo, podemos expressar a3 em função de a6 da seguinte forma:
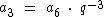
Como:
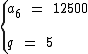
Temos:
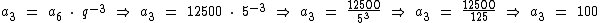
Portanto:
 O valor do terceiro termo é 100.
O valor do terceiro termo é 100.
 5) Se somarmos os 7 primeiros termos da P.G. ( 7, 21, ... ) qual será o valor obtido?
5) Se somarmos os 7 primeiros termos da P.G. ( 7, 21, ... ) qual será o valor obtido?
A razão da sucessão pode ser obtida da seguinte forma:
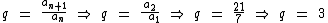
Para a solução do exercício temos então as seguintes variáveis:
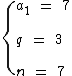
Calculando temos:
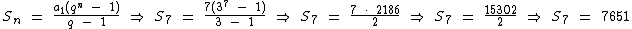
Logo:
 O valor obtido ao somarmos os 7 primeiros termos da referida P.G. será de 7651.
O valor obtido ao somarmos os 7 primeiros termos da referida P.G. será de 7651.
 6) Ao somarmos o segundo, o quinto e o sexto termo de uma P.G. obtemos 400. Ao somarmos o terceiro, o sexto e o sétimo termo, obtemos o dobro disto. Quanto obteremos se somarmos os três primeiros termos desta progressão?
6) Ao somarmos o segundo, o quinto e o sexto termo de uma P.G. obtemos 400. Ao somarmos o terceiro, o sexto e o sétimo termo, obtemos o dobro disto. Quanto obteremos se somarmos os três primeiros termos desta progressão?
A partir do enunciado montamos duas equações:
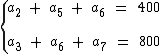
Podemos escrevê-las em função do primeiro termo para ficarmos com apenas duas variáveis, a1 e q:
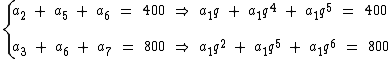
Repare que podemos colocar q em evidência na segunda equação:
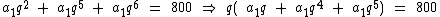
Perceba que esta providência nos permitirá encontrar o valor de q, já que o valor que está entre parênteses é exatamente igual à primeira equação:
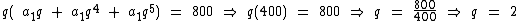
Substituindo q pelo seu valor na primeira equação, já com os termos colocados em função de a1, encontraremos o valor deste termo:
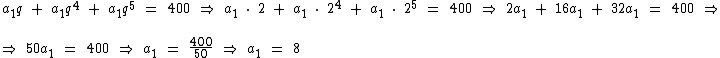
Finalmente, sabendo que a1 = 8 e que q = 2, podemos calcular o valor da soma dos três primeiro termos:
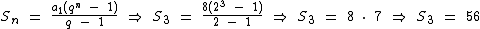
Portanto:
 A soma dos três primeiros termos desta progressão é igual a 56.
A soma dos três primeiros termos desta progressão é igual a 56.
 7) Qual é o produto da multiplicação dos 5 primeiros termos da P.G. ( 6, 9, ... )?
7) Qual é o produto da multiplicação dos 5 primeiros termos da P.G. ( 6, 9, ... )?
A seguir obtemos a razão da sucessão:
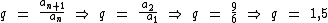
As variáveis que dispomos para a solução do exercício são:
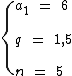
Aplicando a fórmula para o cálculo do produto dos termos de uma progressão geométrica temos:
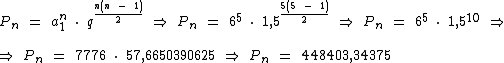
Enfim:
 O produto dos cinco primeiros termos da referida P.G. é de 448403,34375.
O produto dos cinco primeiros termos da referida P.G. é de 448403,34375.
 8) O sétimo termo de uma P.G. é igual a 1458 e o nono é igual a 13122. O primeiro é igual a quanto?
8) O sétimo termo de uma P.G. é igual a 1458 e o nono é igual a 13122. O primeiro é igual a quanto?
Do enunciado temos:
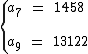
Sabemos que o termo a8 é média geométrica dos termos a7 e a9 conforme abaixo:
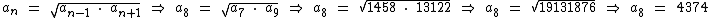
Podemos calcular a razão da progressão, pois sabemos que podemos obtê-la como a seguir:
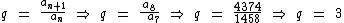
Sabendo que a razão q = 3, podemos encontrar a1 que se localiza 6 termos à esquerda de a7. Então temos:
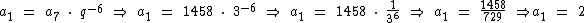
Logo:
 O primeiro termo desta P.G. é igual a 2.
O primeiro termo desta P.G. é igual a 2.
 9) Qual é a soma dos termos da P.G. ( 9, 27, ..., 19683)?
9) Qual é a soma dos termos da P.G. ( 9, 27, ..., 19683)?
Dividindo o segundo termo da P.G. pelo primeiro, obteremos a sua razão:
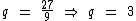
Os dados que dispomos são:
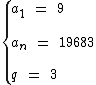
Primeiramente precisamos obter o número de itens da sucessão:
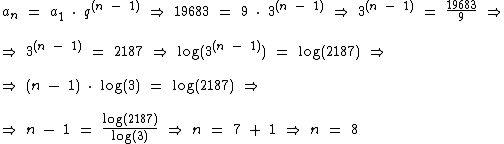
Agora já dispomos de todos os dados necessários ao cálculo da soma dos termos:
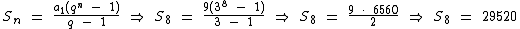
Assim sendo:
 A soma dos termos da P.G. ( 9, 27, ..., 19683) é igual a 29520.
A soma dos termos da P.G. ( 9, 27, ..., 19683) é igual a 29520.
 10) Qual é o valor de x na P.G.(x - 40, x, x + 200)?
10) Qual é o valor de x na P.G.(x - 40, x, x + 200)?
Como x é média geométrica entre x - 40 e x + 200 temos:
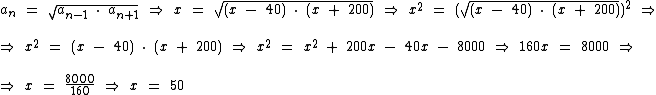
Portanto:
 O valor de x na progressão geométrica é 50.
O valor de x na progressão geométrica é 50.






