Análise Combinatória - Fatorial
Ao produto dos números naturais começando em n e decrescendo até 1 denominamos de fatorial de n e representamos por n!.
Segundo tal definição, o fatorial de 5 é representado por 5! e lê-se 5 fatorial.
5! é igual a 5 . 4 . 3 . 2 . 1 que é igual a 120, assim como 4! é igual a 4 . 3 . 2 . 1 que é igual a 24, como 3! é igual a 3 . 2 . 1 que é igual a 6 e que 2! é igual a 2 . 1 que é igual a 2.
Por definição tanto 0!, quanto 1! são iguais a 1.
Abaixo, no final da página, temos uma tabela com os 28 primeiros fatoriais. Repare que apesar do número 27 ser relativamente baixo, o seu fatorial possui 29 dígitos!
Escrevendo um fatorial a partir de um outro fatorial menor
Vimos que 5! é equivalente a 5 . 4 . 3 . 2 . 1, mas note que também podemos escrevê-lo de outras formas, em função de fatoriais menores, tais como 4!, 3! e 2!:
- 5! = 5 . 4!
- 5! = 5 . 4 . 3!
- 5! = 5 . 4 . 3 . 2!
Para um fatorial genérico temos:
n! = n . (n - 1)! = n . (n - 1) . (n - 2)! = n . (n - 1) . (n - 2) . (n - 3) . ... . 1!
Observe atentamente os exemplos seguintes:
- (n + 3)! = (n + 3) . (n + 2)!
- (n + 3)! = (n + 3) . (n + 2) . (n + 1)!
- (n + 1)! = (n + 1) . n!
Vamos atribuir a n o valor numérico 6, para termos uma visão mais clara destas sentenças:
- 9! = 9 . 8!
- 9! = 9 . 8 . 7!
- 7! = 7 . 6!
Estes conceitos são utilizados em muitos dos problemas envolvendo fatoriais.
Simplificação envolvendo fatoriais
Observe a fração abaixo:
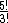
Vimos que 5! é equivalente a 5! = 5 . 4 . 3!. Então podemos escrever a fração da seguinte forma:
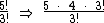
Agora podemos simplificar o 3! do numerador com o 3! do denominador. Temos então:
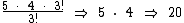
Veja outros exemplos:
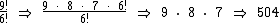
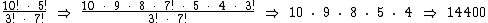


Gerando uma sequência de números compostos consecutivos a partir de um fatorial
Na página onde falamos sobre múltiplos de um número natural foi explicado que se a um número que é múltiplo de n, somarmos n ou qualquer um dos seus múltiplos, iremos obter como resultado um número que também é múltiplo de n.
3! + 2 = 3 . 2 . 1 + 2 = 6 + 2 = 8
3! + 3 = 3 . 2 . 1 + 3 = 6 + 3 = 9
Repare que 8, resultado da soma de 6 com 2, é divisível por 2, assim como 6. O mesmo ocorrendo com 9, resultado da soma de 6 com 3, que também é divisível por 3.
Como 8 e 9 são múltiplos de algum fator de 3!, temos que eles formam uma sequência de dois números compostos (não primos) consecutivos a partir do fatorial de três.
3! possui três fatores, mas só podemos considerar os fatores maiores que 1, por isto só pudemos somar dois e três. Note neste exemplo, que se somássemos 3! + 1, iríamos obter 7, que não é um número composto. Sete é um número primo.
Exemplos de problemas envolvendo fatoriais
 Qual deve ser o valor numérico de n para que a equação (n + 2)! = 20 . n! seja verdadeira?
Qual deve ser o valor numérico de n para que a equação (n + 2)! = 20 . n! seja verdadeira?
O primeiro passo na resolução deste problema consiste em escrevermos (n + 2)! em função de n!, em busca de uma equação que não mais contenha fatoriais:
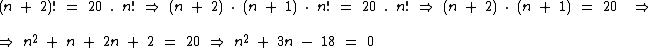
Conforme explicado na página onde tratamos sobre o cálculo rápido das raízes de equações do segundo grau, podemos resolver rapidamente esta equação respondendo à seguinte pergunta: Quais são os dois números cuja soma é igual a -3 e cujo produto é igual -18?
Rapidamente concluímos que as raízes procuradas são -6 e 3, mas como não existe fatorial de números negativos, já que eles não pertencem ao conjunto dos números naturais, ficamos apenas com a raiz igual a 3.
Portanto:
 O valor numérico de n para que a equação seja verdadeira é igual a 3.
O valor numérico de n para que a equação seja verdadeira é igual a 3.
 A partir de fatoriais, obtenha uma sequência com sete números compostos consecutivos.
A partir de fatoriais, obtenha uma sequência com sete números compostos consecutivos.
Como eu devo obter 7 números compostos consecutivos na sequência, eu preciso partir ao menos de 8!:
8! = 8 . 7 . 6. 5 . 4 . 3 . 2 . 1 = 40320
Como 8! é igual a 40320, o primeiro número da sequência será 40320 + 2 = 40322 e o último será 40320 + 8 = 40328.
Logo:
 A sequência 40322, 40323, 40324, 40325, 40326, 40327 e 40328 satisfaz as condições do enunciado.
A sequência 40322, 40323, 40324, 40325, 40326, 40327 e 40328 satisfaz as condições do enunciado.

Tabela com os fatorais de 0 a 27
| n | n! |
|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5040 |
| 8 | 40320 |
| 9 | 362880 |
| 10 | 3628800 |
| 11 | 39916800 |
| 12 | 479001600 |
| 13 | 6227020800 |
| 14 | 87178291200 |
| 15 | 1307674368000 |
| 16 | 20922789888000 |
| 17 | 355687428096000 |
| 18 | 6402373705728000 |
| 19 | 121645100408832000 |
| 20 | 2432902008176640000 |
| 21 | 51090942171709440000 |
| 22 | 1124000727777607680000 |
| 23 | 25852016738884976640000 |
| 24 | 620448401733239439360000 |
| 25 | 15511210043330985984000000 |
| 26 | 403291461126605635584000000 |
| 27 | 10888869450418352160768000000 |
