Número de Ouro
Observe a figura ao lado na qual a junção de dois segmentos de reta forma em um terceiro segmento de reta:
Observe a figura ao lado na qual a junção de dois segmentos de reta forma em um terceiro segmento de reta:
Digamos que a medida de tais segmentos respeitem a seguinte proporção:
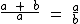
Agora perguntamos:
 Qual é o valor da razão de a para b ou da razão de a + b para a?
Qual é o valor da razão de a para b ou da razão de a + b para a?
Você a de convir conosco que há infinitos valores de a e b cuja razão resulta no valor procurado, então por conveniência vamos arbitrar que b = 1 o que nos leva à seguinte proporção:
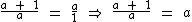
Embora possa não parecer, estamos diante de uma equação do segundo grau cujas raízes obtemos a seguir:
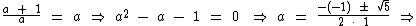
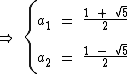
Lembre-se que estamos trabalhando com a medida de segmentos de reta e sendo assim, vamos desprezar a raiz a2, visto que a medida de um segmento de reta não pode ser negativa.
Visto que arbitramos b = 1, a razão de a para b é igual ao próprio valor de a: 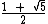
O número de ouro é uma razão representada pelo número irracional Φ (Phi).
Este número irracional é representado pela tela grega Φ (Phi):
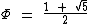
Ou:
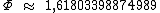
Assim como acontece com vários outros números, o número Φ também pode ser obtido de outras maneiras.
Esta fração contínua também resulta em Φ:
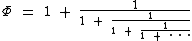
Abaixo temos outra forma de obtê-lo:
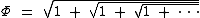
No estudo da sequência de Fibonacci vimos que a divisão de F(n) por F(n - 1), para n > 1, tende a Φ à medida que n aumenta.
Como último exemplo, podemos recorrer à trigonometria para calcularmos valor de Φ:
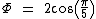
Retângulo de Ouro

Em um retângulo dourado, como o da figura ao lado, a razão de um lado maior para um lado menor é igual a Φ:
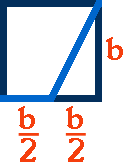
A partir de um quadrado qualquer podemos facilmente obter um retângulo de ouro e para que você entenda como isto é possível, vamos analisar a figura a seguir:
Note que temos um quadrado cujo lado inferior foi dividido em duas partes igual a b/2. b é a medida de cada um dos lados deste quadrado.
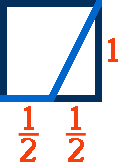
Para facilitar as explicações vamos assumir que b = 1, mas note que poderíamos utilizar qualquer outro valor positivo.
Observe que a medida total da linha em azul claro é igual a 1/2, referente à metade do lado inferior, mais a medida da linha diagonal.
Veja que esta diagonal corresponde à hipotenusa do triângulo retângulo formado pelo lado direito do quadrado, pela metade em azul escuro da base do quadrado e pela própria diagonal em azul claro.
Vamos recorrer ao teorema de Pitágoras para calcular o valor desta hipotenusa:
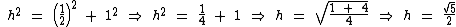
Então a medida da linha em azul claro é igual a:
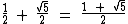
Percebeu qual foi o valor obtido?
Exatamente o valor de Φ:
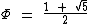
Como já temos a altura do retângulo medindo 1 unidade, para que tenhamos a base medindo Φ unidades, as medidas de um retângulo áureo, precisamos "derrubar" a diagonal em azul claro colocando-a na horizontal.

Com o auxílio de um compasso, colocamos a sua ponta seca no ponto médio da base do quadrado e traçamos um arco:

Agora precisamos aumentar o segmento da base da até o arco:

Finalmente apagamos o lado direito do quadrado e completamos o traçado do retângulo de ouro:
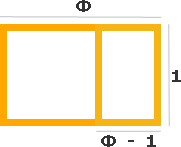
É interessante observar que o retângulo que utilizamos para que, juntamente com o quadrado, formássemos um retângulo de ouro, também é um retângulo dourado:
Como um lado maior deste retângulo mede 1 unidade e um lado menor mede Φ - 1 unidades, a razão do lado maior para o lado menor também é igual a Φ:
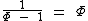
O contrário também é verdadeiro. Se partirmos de um retângulo dourado e o dividirmos em duas partes, sendo uma um quadrado e a outra um retângulo, este retângulo também será um retângulo áureo.
