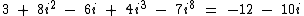No desenvolvimento da multiplicação de números complexos, em um dado momento para darmos continuidade na realização da operação necessitamos saber que i² = -1, mas como podemos simplificar a expressão abaixo?

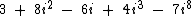
Para fazê-lo precisamos conhecer o valor de outras potências de i.

Vamos observar a figura abaixo:

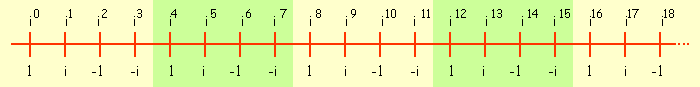
Nela notamos que as quatro primeiras potências têm resultados idênticos às respectivas quatro potências seguintes, o mesmo ocorre entre estas e as próximas quatro potências e assim por diante repetindo o ciclo a cada quatro potências.

Tal ocorrência obedece a uma lei de formação muito simples.

Considere o resto da divisão do expoente da potência de i por 4.

Para um resto r igual a 0, 1, 2 ou 3, temos uma potência igual a 1, i, -1 ou -i respectivamente:

r	ir
0	i0 = 1
1	i1 = i
2	i2 = -1
3	i3 = -i

Por exemplo, para o expoente 8 temos que i⁸ = 1, pois o resto da divisão de 8 por 4 é igual 0, já que oito é divisível por quatro, e segundo a tabela acima, para um resto igual a 0 temos que a potência i⁸ é igual a 1:

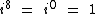
Simplificando a Expressão Exemplo

Agora que sabemos que i² = -1, i³ = -i e i⁸ = 1, podemos simplificar a expressão que vimos no começo deste artigo:

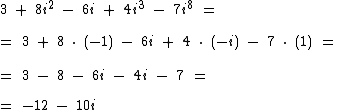
Portanto: