Exercícios resolvidos - Conjuntos Numéricos Fundamentais
Para maiores informações teóricas sobre este assunto veja também:Conjuntos Numéricos Fundamentais
1) A quais conjuntos numéricos fundamentais não pertence o número 
?
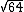Sabemos que 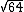é igual a 8.
A trabalharmos com conjuntos utilizamos o símbolo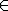 
para indicar que um elemento pertence a um conjunto, assim como utilizamos o símbolo 
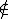para indicar que um elemento não pertence a um determinado conjunto. Assim sendo temos:
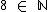(oito pertence ao conjunto dos números naturais), pois como sabemos 8 é um número natural;
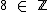(oito pertence ao conjunto dos números inteiros), pois é sabido que os números naturais são um subconjunto dos números inteiros, sabemos que 
;
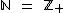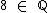(oito pertence ao conjunto dos números racionais), pois podemos representar 8 como 
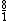que é uma fração com numerador e denominador pertencentes ao conjunto dos números naturais, condição necessária para que um número pertença ao conjunto dos números racionais.
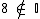(oito não pertence ao conjunto dos números irracionais), pois como 64 é um número natural que é também um quadrado perfeito, 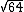não é um número irracional, pois 
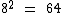. De fato 8 ou 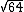jamais poderiam ser irracionais, pois como visto acima, eles são racionais ( 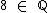) e nenhum número racional é também irracional e vice-versa.
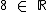(oito pertence ao conjunto dos números reais), pois o conjunto dos números racionais é um subconjunto dos números reais ( 
).
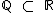Através do diagrama visto na parte teórica, facilmente podemos resolver este problema de forma visual ao identificarmos que 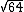(ou 8) é um número natural.
Portanto:
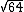não pertence ao conjunto dos números irracionais ( 
).
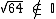2) A quais conjuntos numéricos fundamentais não pertence o número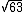 
?
3) Existe raiz quadrada de número primo que não seja irracional?
Vimos que a raiz quadrada de um número natural pode ser tanto natural, quanto irracional, mas para que a raiz seja natural, o número deve ser um quadrado perfeito.
Para que um número seja primo é preciso que além de natural ele possua exatamente apenas dois divisores distintos, o número um e ele próprio.
Falando em termos de conjuntos, a intersecção do conjunto dos números primos com o conjunto natural dos quadrados perfeitos é igual ao conjunto vazio (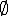 
), ou seja, um número primo não pode ser um quadrado perfeito e vice-versa.
Assim sendo:
Não existe raiz quadrada de número primo que não seja irracional.
4) Se a e b são números pertencentes a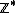 
e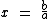 
, a quais conjuntos numéricos fundamentais podemos afirmar com certeza que x pertence, quaisquer que sejam os valores de a e b?
A partir do enunciado, podemos chamar de A o conjunto ao qual x pertence e representá-lo por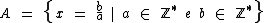 
Sabemos que, dentre outras formas, podemos representar o conjunto dos números racionais por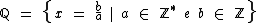 
Como podemos observar, A é um subconjunto de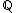 
, isto é,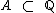 
Sabemos também que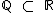
Assim sendo:
Podemos afirmar com certeza qu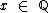e 
e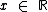 
.
5) Se A é um subconjunto de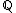 
e B está contido em 
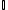, a intersecção destes conjuntos possui infinitos elementos?
Do enunciado temos que:
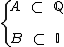
É sabido que tal como óleo e água, os elementos dos conjuntos dos números racionais e irracionais não se misturam, ou seja, a intersecção entre ele é o conjunto vazio, pois não há um único número sequer que sendo racional seja também irracional e vice-versa, os elementos destes conjuntos são mutuamente exclusivos: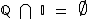 
Portanto:
A intersecção entre os conjuntos A e B não possui infinitos elementos.
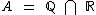6) Se 
e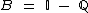 
, tem-se que 
?
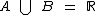