Exercícios resolvidos - Potenciação e Radiciação
Para maiores informações teóricas sobre este assunto veja também:Exponenciação
 1) Calcule 4-2.
1) Calcule 4-2.
Na parte teórica estudamos que:
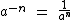
Então:
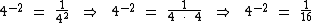
Logo:
 4-2 = 1/16.
4-2 = 1/16.
 2) Calcule menos seis elevado à quarta potência.
2) Calcule menos seis elevado à quarta potência.
Temos uma potência de base -6 e expoente 4, logo:
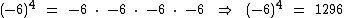
Embora bastante simples, este exercício possui um ponto que deve ser bem observado. Note que a potência foi escrita como (-6)4 e não como -64. Isto porque se não tivéssemos este cuidado, apenas o 6 seria elevado à quarta potência. Veja como ficaria:
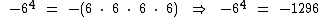
Portanto:
 Menos seis elevado à quarta potência é igual a 1296.
Menos seis elevado à quarta potência é igual a 1296.
 3) Calcule 85 - (-5)2 + 31 + 40 + 2-1.
3) Calcule 85 - (-5)2 + 31 + 40 + 2-1.
Apenas para facilitar a visualização da resolução das potências, vamos calculá-las separadamente da expressão:
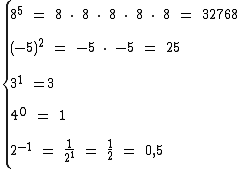
Agora montamos novamente a expressão com os resultados obtidos:
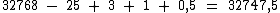
Então:
 85 - (-5)2 + 31 + 40 + 2-1 = 32747,5.
85 - (-5)2 + 31 + 40 + 2-1 = 32747,5.
 4) Calcule 432 e (43)2.
4) Calcule 432 e (43)2.
No primeiro caso elevamos o 3 ao quadrado, que dá 9 e depois elevamos 4 à nona potência:
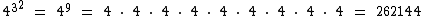
Já no segundo caso elevamos o 4 ao cubo, que dá 64 e depois elevamos 64 à segunda potência:
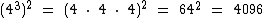
Os cálculos são diferentes porque os parênteses mudam a ordem normal na qual as operações devem ser realizadas.
Logo:
 432 = 262144 e (43)2 = 4096.
432 = 262144 e (43)2 = 4096.
 5) Quais os resultados de 713 : 711 e de 2-4 . 25?
5) Quais os resultados de 713 : 711 e de 2-4 . 25?
Tanto no primeiro caso quanto no segundo, temos bases idênticas. Nestas condições normalmente é melhor trabalharmos na forma de potência e só no final resolvê-la. Na primeira situação temos:
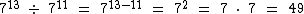
Repare que foi muito mais simples do que se tivéssemos calculado primeiro 713 e depois 711 e em seguida dividido um valor pelo outro.
Vamos ao segundo caso:
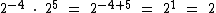
Assim como no primeiro caso, realizamos as operações de forma mais simples do que se tivéssemos resolvido as potências no início dos cálculos, isto sem dizer que normalmente trabalhando desta forma as operações são realizadas mentalmente quando é possível.
Portanto:
 713 : 711 = 49 e 2-4 . 25 = 2.
713 : 711 = 49 e 2-4 . 25 = 2.
 6) Calcule
6) Calcule 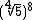 .
.
Vamos resolver este exercício de duas maneiras distintas. Na primeira vamos passar o expoente 8 para dentro do radical e na segunda vamos transformar o radical em uma potência com expoente fracionário.
Passando o expoente 8 para dentro do radical temos:
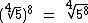
Agora vamos utilizar a propriedade da mudança de índice pela sua divisão e do expoente do radicando por 4:
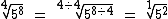
A raiz de índice 1 de um número é igual ao próprio número:
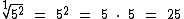
Pela outra forma temos:
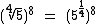
Agora multiplicamos os expoentes e resolvemos a potência:
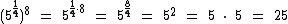
Então:

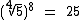 .
.
 7) Calcule
7) Calcule 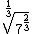 .
.
Podemos resolver este exercício multiplicando índice e expoente, ambos por 3. Isto eliminará as frações e de quebra o radicando:
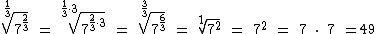
Uma outra forma de resolução é transformarmos o radicando em uma potência de expoente fracionário:
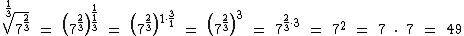
Logo:

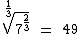 .
.
 8) Calcule
8) Calcule 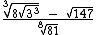 .
.
Inicialmente vamos fatorar 8, 147 e 81:
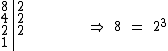
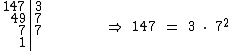
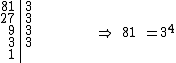
Você pode utilizar a nossa calculadora para decomposição de um número natural em fatores primos, se estiver com duvidas sobre a fatoração.
Após realizarmos as substituições temos:
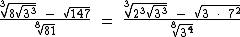
Agora segundo a propriedade da raiz de uma potência, em 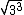 vamos transformar a raiz de uma potência, na potência de uma raiz, tirando o expoente do radicando para fora do radical:
vamos transformar a raiz de uma potência, na potência de uma raiz, tirando o expoente do radicando para fora do radical:
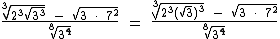
Em 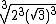 vamos dividir por 3, tanto o índice quanto os expoentes, para eliminarmos o radical:
vamos dividir por 3, tanto o índice quanto os expoentes, para eliminarmos o radical:
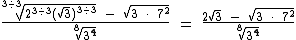
Em  vamos fazer algo semelhante, dividindo por 2, tanto o índice quanto o expoente de 72, para também retirarmos o 7 do radical:
vamos fazer algo semelhante, dividindo por 2, tanto o índice quanto o expoente de 72, para também retirarmos o 7 do radical:
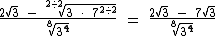
Observe que na realidade tomamos um atalho, pois a operação completa para retirarmos o 7 do radicando seria:
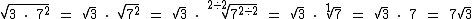
Repare que primeiro separamos a multiplicação no radicando em dois radicais e depois realizamos a divisão por 2.
Continuando, vamos simplificar agora o índice e o expoente de 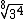 , dividindo-os por 4:
, dividindo-os por 4:
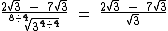
Como 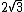 e
e 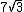 possuem o mesmo radical, podemos subtrair um do outro:
possuem o mesmo radical, podemos subtrair um do outro:
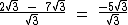
Agora vamos simplificar a fração dividindo numerador e denominador por 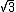 :
:
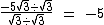
Portanto:

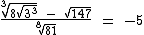 .
.
 9) Extraia a raiz cúbica de 3375 pelo método da fatoração.
9) Extraia a raiz cúbica de 3375 pelo método da fatoração.
Fatorando 3375 temos:
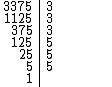
Como 3375 = 33 . 53 temos:
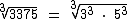
Como ambos os expoentes são divisíveis pelo índice 3 do radicando, pois são iguais a 3, podemos retirar ambos os fatores do radical, dividindo os expoentes pelo índice 3 e repetindo as bases das potências, agora sem o radical:
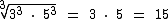
Então:

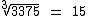 .
.
 10) Simplifique o radical
10) Simplifique o radical 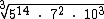 .
.
Para facilitar a explicação vamos iniciar separando os fatores em um radical à parte, todos com o mesmo índice:
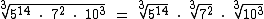
No primeiro radical a divisão de 14 por 3 terá como quociente 4 e como resto 2, então o radical simplificado será a base 5 elevada ao quociente 4 multiplicada pela raiz cúbica de 5 elevado ao resto 2:
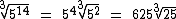
O segundo radical não iremos simplificar, pois o expoente do radicando é menor que o índice do radical, além de serem primos entre si. Se houvesse um divisor comum maior que 1, iríamos dividi-los por este divisor:
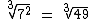
Por fim no último radical, como o expoente é igual ao próprio índice, teremos como fator apenas a base 10:
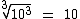
Substituindo os radicais por suas simplificações temos:

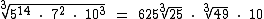 .
.
