Os números de Fibonacci formam uma sequência infinita de números naturais, sendo que a partir do terceiro, os números são obtidos através da soma dos dois números anteriores.

A sequência definida por Fibonacci inicia-se com 1 e 1, mas por convenção pode-se definir F(0) = 0, isto é, pode-se convencionar que a sequência começa em 0 e 1.

Em função do dito acima podemos montar a seguinte tabela com os primeiros 22 números da sequência de Fibonacci:

n	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21
F(n)	0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	987	1597	2584	4181	6765	10946

Na primeira linha temos o índice do número de Fibonacci na sequência e na segunda linha temos o número propriamente dito, por exemplo, para  n = 7  que corresponde ao oitavo número, temos que  F(7) = 13 , ou seja, o oitavo número da série é o número 13.

Veja que de fato, a partir do terceiro número, cada um deles é o resultado da soma dos números anteriores, por exemplo, 10946 = 4181 + 6765.

Cada n-ésimo Número de Fibonacci é Múltiplo de F(n), para n ≥ 1

Vamos tomar como exemplo  n = 3. Como vemos na tabela,  F(3) = 2. Veja que para cada n múltiplo 3, temos que F(n) é múltiplo de F(3), ou seja, múltiplo de 2:

n	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21
F(n)	0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	987	1597	2584	4181	6765	10946

Caso você não tenha compreendido, vamos a este outro exemplo com  n = 7. Na tabela temos que  F(7) = 13. Observe que para cada n múltiplo 7, temos que F(n) é múltiplo de F(7), isto é, múltiplo de 13:

n	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21
F(n)	0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	987	1597	2584	4181	6765	10946

Tanto 377, quanto 10946 são múltiplos de 13.

Como último exemplo veja na tabela o caso de  n = 5:

n	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21
F(n)	0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	987	1597	2584	4181	6765	10946

Note que F(5), F(10), F(15) e F(20) são todos múltiplos de 5.

Soma dos Termos da Sequência de Fibonacci

Veja em qualquer uma das tabelas acima que o termo F(10) = 55.

Qual será a soma de F(0) a F(10)?

Vejamos:

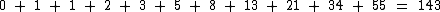
Observe que este total é uma unidade menor que F(12), que é igual a 144. Isto não é uma coincidência, de fato, a soma dos termos de F(0) a F(n) é igual a F(n + 2) - 1:

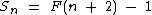
Qual é a soma dos termos de F(0) a F(15)?

Como na tabela F(17) = 1597, temos que:

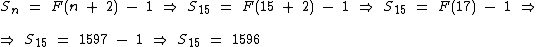
Qual é a soma dos termos dos primeiros números de Fibonacci até o número 10946?

Na tabelas acima vemos que 10946 corresponde a F(21), portanto, para obtermos a soma precisamos saber o valor de F(23).

No caso de F(22) temos:

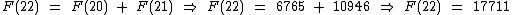
Logo F(23) é igual a:

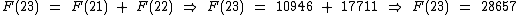
Agora já temos como calcular a soma até o número 10946:

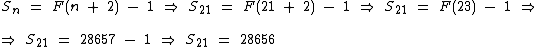
Sendo F(30) = 832040, qual é a soma dos termos de F(0) até F(30)?

Agora a coisa complicou um pouco, visto que desconhecemos o valor de F(29), ainda não sabemos como calcular o valor de F(31), nem de F(32) com as informações que tivemos até aqui.

Qual será a solução então?

Simples, ampliar o nosso conhecimento!

O Número de Ouro e a Sequência de Fibonacci

O número de ouro ou proporção áurea é uma razão representada pelo número Φ (Phi). 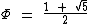ou aproximadamente 1,61803398874989. Phi é um número irracional.

A divisão de F(n) por F(n - 1), para n > 1, tende a Φ à medida que n aumenta, por exemplo:

Se dividirmos F(2) por F(1) vamos obter 2, que nem chega a lembrar o numero Φ:

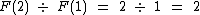
Se considerarmos um n um pouco maior, como por exemplo 15, vamos obter aproximadamente 1,618037135 que é um valor que já nos mostra para qual valor estamos caminhando:

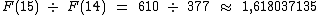
Se à medida que n aumenta, a razão de F(n) por F(n - 1) tende a Φ, então podemos utilizar esta propriedade para rapidamente calcularmos o valor de F(n + 2), quando precisamos calcular a soma dos termos de uma série de números de Fibonacci de F(0) até F(n) e só conhecemos este valor F(n).

Por exemplo, para calcularmos a soma dos termos da sequência de Fibonacci até 55, se não soubermos que o número anterior é o 34, podemos multiplicar 55 por Phi duas vezes (ou multiplicar por Phi²), que dará aproximadamente 143,99, ou seja, o segundo número após 55 será o número 144, note que arredondamos o valor 143,99, neste caso para maior. A soma será então 143.

Agora já temos como calcular F(32) que ficou pendente no problema acima.

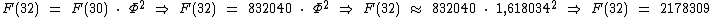
Logo, a soma dos termos de F(0) até F(30) é igual a:

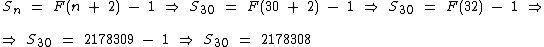
Como Obter o n-ésimo Termo da Sequência de Fibonacci?

A fórmula de Binet pode ser utilizada para o cálculo do n-ésimo número da sequência de Fibonacci:

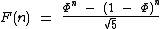
Vamos calcular F(21) que, como vimos nas tabelas acima, é igual a 10946:

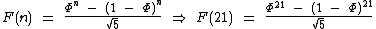
Para continuar os cálculos vamos utilizar um valor aproximado de Φ. Utilizaremos Φ = 1,618034:

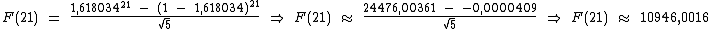
Como a sequência de Fibonacci é formada por números naturais, o número natural mais próximo de 10946,0016 é 10946, portanto F(21) = 10946.

Como trabalhamos com potências elevadas, normalmente utilizamos calculadoras científicas na realização destes cálculos, neste caso podemos utilizar toda precisão da mesma ao utilizarmos o valor de Φ. Lembre-se que: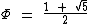

Com o auxílio de uma calculadora, o número F(32) que precisamos calcular no problema anterior, também pode ser obtido através da fórmula de Binet:

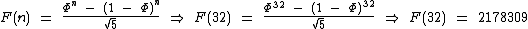
Visto que (1 - Φ)ⁿ tende a zero à medida que n aumenta, podemos simplificar a fórmula de Binet eliminando este termo:

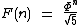
Calculando o número F(32) temos:

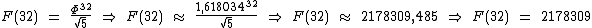
Note que a fórmula simplificada pode ser utilizada para qualquer valor de n, mesmo para n muito pequeno:

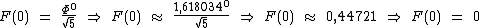
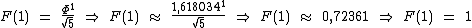
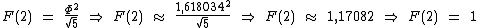
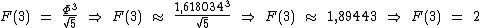
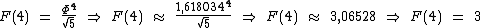
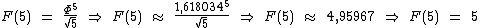
Observe que os números sempre são arredondados para o número natural mais próximo.

Precisamos realizar o arredondamento, principalmente por causa da eliminação do termo (1 - Φ)ⁿ, mas também por causa das aproximações dos números utilizados nos cálculos.

Como Saber o Número de Ordem de um Determinado Termo da Sequência de Fibonacci?

Podemos utilizar a fórmula simplificada que vimos acima para, para dado um número de Fibonacci, identificar a sua posição na sequência, para qualquer número de Fibonacci maior que 1.

Para isto vamos isolar n:

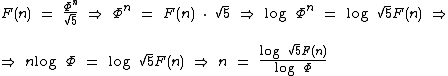
Vamos mostrar a utilização da fórmula abaixo para descobrirmos a posição de alguns números na sequência de Fibonacci:

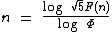
Vejamos alguns exemplos da utilização desta fórmula:

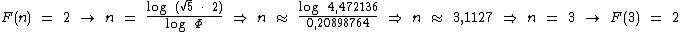
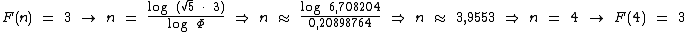
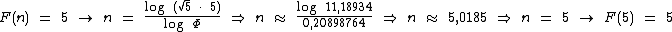
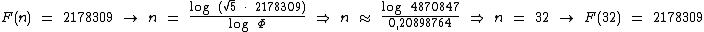
Como pode ser observado, o valor de n é arredondado para o número natural mais próximo, acima ou abaixo, visto que a posição de um número na sequência de Fibonacci também é um número natural.