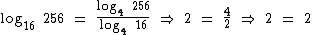Logaritmo
Ao estudarmos a exponenciação ou potenciação aprendemos que, por exemplo, o produto de 3 por 3, que é igual a 9, pode ser representado na forma de uma potência pela seguinte sentença matemática:
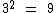
Utilizando a notação dos logaritmos também podemos representá-la assim:
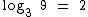
Pela nomenclatura dos logaritmos nesta sentença temos:
2 é o logaritmo de 9 na base 3;
3 é a base do logaritmo;
9 é o logaritmando.
Genericamente de forma simbólica temos a seguinte definição de logaritmo:
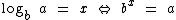
Para os números reais positivos a e b, com b ≠ 1, denomina-se logaritmo de a na base b o expoente real x, tal que bx = a
Vejamos a sentença abaixo:
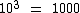
O expoente desta potência, no caso 3, é o logaritmo de 1000 que podemos representar assim:
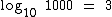
Como você já sabe, na representação de alguns símbolos matemáticos, alguma parte muito utilizada em geral é omitida. Como exemplo temos que 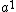 pode, de forma simplificada, ser expresso como
pode, de forma simplificada, ser expresso como  , com a omissão do expoente 1.
, com a omissão do expoente 1.
Um outro exemplo pode ser uma raiz quadrada qualquer, que em vez de a expressarmos como 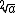 , utilizamos apenas
, utilizamos apenas 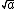 .
.
Ao trabalharmos com logaritmos na base 10 normalmente a omitimos, então em vez de 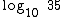 , utilizamos
, utilizamos 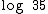 , que como você pode notar, teve a base 10 omitida. Estas simplificações têm por objetivo simplificar tanto a escrita, quanto a leitura de tais símbolos, facilitando assim a compreensão de tais expressões.
, que como você pode notar, teve a base 10 omitida. Estas simplificações têm por objetivo simplificar tanto a escrita, quanto a leitura de tais símbolos, facilitando assim a compreensão de tais expressões.
Assim sendo a expressão 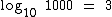 em geral é escrita como
em geral é escrita como 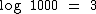
Propriedades dos Logaritmos
Considerando a, b, c, M e N números reais positivos, com b ≠ 1 e c ≠ 1, temos as seguintes propriedades dos logaritmos:

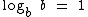
Para qualquer logaritmo cujo logaritmando seja igual a base, o logaritmo será igual a 1.
Isto fica claro no exemplo abaixo, já que todo número real elevado a 1 é igual a ele próprio:
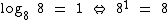

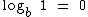
Qualquer logaritmo cujo logaritmando seja igual a 1, o logaritmo será igual a 0.
Veja abaixo um exemplo onde arbitramos 6 para um dos possíveis valores de b:
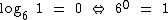

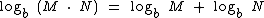
O logaritmo na base b do produto de M por N é igual à soma do logaritmo na base b de M com o logaritmo na base b de N.
Vamos tomar como exemplo o 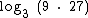 .
.
Pela propriedade do logaritmo de um produto temos:
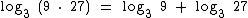
Como vimos acima o 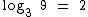 , pois a base 3 elevada ao expoente 2 é igual a 9:
, pois a base 3 elevada ao expoente 2 é igual a 9:
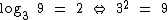
Claramente o 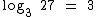 , já que devemos elevar a base 3 ao expoente 3 para obtermos 27:
, já que devemos elevar a base 3 ao expoente 3 para obtermos 27:
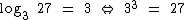
Realizando a substituição destes logaritmos na expressão original temos:
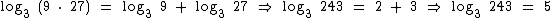
Então chegamos a:
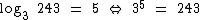
O logaritmo de 243 na base 3 é igual a 5, pois este é o expoente ao qual 3 precisa ser elevado para obtermos 243.

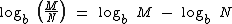
O logaritmo na base b do quociente de M por N é igual à diferença entre o logaritmo na base b de M e o logaritmo na base b de N.
Agora vamos utilizar o 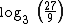 neste outro exemplo.
neste outro exemplo.
Segundo a propriedade do quociente de um logaritmo temos:
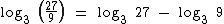
Já que como visto o 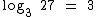 e
e 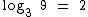 temos que:
temos que:
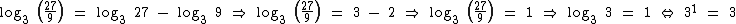
O logaritmo de 3 na base 3 é igual a 1, já que este é o expoente ao qual a base 3 é elevada para 3 ser obtido.

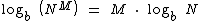
Para qualquer valor real M, o logaritmo na base b da potência NM é igual ao produto do expoente M pelo logaritmo na base b de N, a base da potência.
Calculemos o logaritmo de 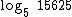 .
.
Ao decompormos 15625 em fatores primos iremos obter 56:
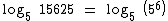
De acordo com a propriedade do logaritmo de uma potência temos:
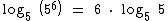
O log5 5 é igual a 1, pois 51 = 5, portanto:
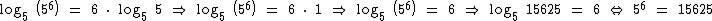
O logaritmo de 15625 na base 5 é igual a 6, visto que este é o expoente ao qual 5 deve ser elevado para obtermos 15625.

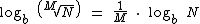
Para qualquer valor natural M, não nulo, o logaritmo na base b da raiz 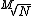 é igual ao produto do inverso do índice M pelo logaritmo na base b de N, o radicando da raiz.
é igual ao produto do inverso do índice M pelo logaritmo na base b de N, o radicando da raiz.
Vamos calcular o logaritmo da raiz cúbica de 343 na base 7.
Pela propriedade do logaritmo de uma raiz, temos que:
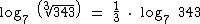
O log7 343 é igual a 3, pois 73 = 343, logo:
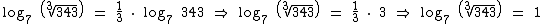
O 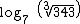 é igual a 1, como já era de se esperar, já que 73 = 343, obviamente
é igual a 1, como já era de se esperar, já que 73 = 343, obviamente 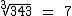 , então
, então 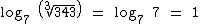 , pois 71 = 7.
, pois 71 = 7.

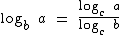
Esta é uma propriedade muito importante, pois através dela podemos realizar a mudança da base de um logaritmo.
Como exemplo vamos mudar o logaritmo de log4 256 para a base 16:
Segundo a propriedade da mudança de base temos:
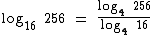
Vamos realizar a conferência deste resultado, verificando se a igualdade é verdadeira. Para isto nós sabemos que:
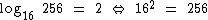
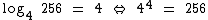

Portanto, substituindo tais logaritmos confirmamos a igualdade: