Vimos que os logaritmos na base 10 podem ser expressos sem se explicitar a base, assim o log₁₀ 1000 pode ser expresso simplesmente por log 1000.

Na introdução aos logaritmos vimos também que o logaritmo de 1000 na base 10 é igual a 3, isto é o log 1000 = 3, isto porque 10³ = 1000.

1000 é uma potência de 10 com expoente 3. Veja que o logaritmo de 1000 é o expoente da potência de 10, então para um expoente N, o log 10^N = N.

Vamos observar a tabela abaixo para alguns valores inteiros de N:

N	log 10N = N
-5	log 10-5 = -5	10-5 = 0,00001
-4	log 10-4 = -4	10-4 = 0,0001
-3	log 10-3 = -3	10-3 = 0,001
-2	log 10-2 = -2	10-2 = 0,01
-1	log 10-1 = -1	10-1 = 0,1
0	log 100 = 0	100 = 1
1	log 101 = 1	101 = 10
2	log 102 = 2	102 = 100
3	log 103 = 3	103 = 1000
4	log 104 = 4	104 = 10000
5	log 105 = 5	105 = 100000

Note que nesta tabela só temos potências de dez com expoente inteiro, seja ele negativo, nulo ou positivo.

Se dela tomarmos duas linhas adjacentes, as linhas com N = 2 e N = 3, por exemplo, vemos que o log 100 = 2 e o log 1000 = 3. Isto quer dizer que o logaritmo de qualquer número real maior que 100 e menor que 1000 é maior que 2 e menor que 3.

Ainda pela tabela, se considerarmos o log 0,00001 = -5 e o log 0,0001 = -4, de forma análoga temos que o logaritmo de qualquer número real maior que 0,00001 e menor que 0,0001 é maior que -5 e menor que -4.

Seguindo este raciocínio, então o logaritmo de 50 deve ser 1 vírgula alguma coisa, pois 50 está entre 10 e 100, que têm o respectivo logaritmo: 1 e 2.

O logaritmo de 50, na base 10, é aproximadamente 1,698970.

De fato 1 < 1,698970 < 2 já que 10¹ < 50 < 10².

Característica e Mantissa

O log 50 é um número decimal que pode ser separado em duas partes. Uma parte inteira e outra decimal.

À parte inteira damos o nome de característica, à parte decimal denominamos mantissa.

Obtendo a Característica de um número real maior ou igual a um

A característica do logaritmo decimal de um número real maior ou igual a 1 é igual ao número de algarismos da parte inteira subtraída de uma unidade.

Como vimos, o número 50 possui dois algarismos na parte inteira, por isto a sua característica é igual a 1.

A característica do logaritmo decimal de 345,67 é igual a 2, pois na parte inteira este número possui 3 algarismos.

Obtendo a Característica de um número real maior que zero e menor que um

Para obtermos a característica do logaritmo decimal de um número real maior que zero e menor que um, contamos o número de zeros antes do primeiro algarismo diferente de zero. A característica é o valor simétrico desta contagem, ou seja, é a contagem com o sinal de negativo, já que o logaritmo decimal de um número menor que um e maior que zero é negativo.

Lembre-se que não existe logaritmo de número negativo.

Qual é a característica do log 0,000504?

Veja que o número 0,000504 possui um zero antes da vírgula e mais três depois dela e antes do primeiro algarismo diferente de zero que é o 5. Por isto a característica do número 0,000504 é -4.

Logaritmo na Forma Mista ou Preparada

A mantissa aproximada do log 0,000504 é 702431, então podemos dizer que o log 0,000504 = -4 + 0,702431, na forma mista.

Veja que na forma mista ou preparada, escrevemos a características e a mantissa como os termos de uma adição. Nesta forma também podemos expressar assim o logaritmo de log 0,000504:

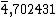
Note que realizamos um traço sobre a característica negativa, semelhante ao vinculum utilizado na escrita de números romanos.

Logaritmo na Forma Negativa

Se você calcular o log 0,000504 em uma calculadora científica irá obter aproximadamente o seguinte valor:

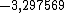
Note que ele difere do valor considerado anteriormente. Por quê?

Porque anteriormente o log 0,000504 estava representado na sua forma preparada e agora ele está na sua forma negativa. Esta é a forma utilizada pelas calculadoras.

Convertendo Logaritmos na Forma Preparada para a Forma Negativa

Para conversão de 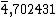em 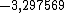devemos tratar a característica e a mantissa separadamente.

A característica 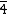passa para -3 simplesmente se somando 1 ao -4 da parte inteira:

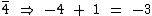
Em relação à mantissa subtraímos de 1 o 0,702431 referente à parte decimal:

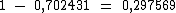
O logaritmo resultante na forma negativa será a subtração das novas partes obtidas:

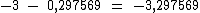
Caso só tenhamos a característica, isto é, a mantissa seja zero, a conversão é mais simples. 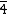na forma preparada é igual a 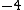na forma negativa.

Convertendo Logaritmos na Forma Negativa para a Forma Preparada

A conversão de 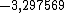em 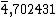também e realizada se tratando a característica e a mantissa separadamente.

Da parte inteira -3 subtraímos 1, que resulta em -4 e escrevemos a característica utilizando o traço sobre este número sem o sinal de negativo:

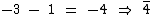
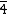é a característica na forma mista.

A mantissa é obtida subtraindo de 1 a parte decimal:

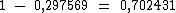
O logaritmo resultante na forma preparada será a junção da característica 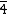com a mantissa 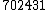, ou seja:

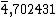
No caso de números inteiros o procedimento é simplificado. Se ao invés de 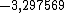, tivéssemos apenas o inteiro 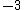, na forma preparada teríamos simplesmente .

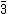E como obtemos a mantissa de um logaritmo?

Isto foi visto quando apresentamos a tábua de logaritmos decimais.