Polinômios
Na página sobre termos algébricos explicamos o que são monômios semelhantes e em seguida tratamos a sua soma e subtração.
A adição ou subtração algébrica de monômios é denominada polinômio.
Vejamos alguns exemplos de polinômios:

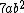

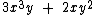

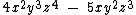

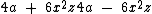

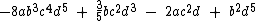
No primeiro exemplo temos um polinômio de apenas um monômio. Os demais possuem vários monômios, estes monômios são denominados termos do polinômio.
O segundo exemplo é um polinômio de dois termos: 3x3y e 2xy2.
Grau de um Polinômio
O grau de um polinômio reduzido, não nulo, é o grau do seu termo de maior grau.
O polinômio -5x4 + 14x5y2 - 7x3y2 é do grau 7, pois o seu termo de maior grau é o segundo, que é do grau 7.
O polinômio 4a2b3 + 5a5 é do grau 5, pois ambos os termos do polinômio são deste grau.
Grau de um Polinômio em Relação a uma Certa Incógnita
Em relação à variável x o polinômio -5x4 + 14x5y2 - 7x3y2 é do grau 5, pois o termo de maior grau nesta variável é do grau 5, que é o segundo termo.
Analisando o mesmo polinômio em relação à variável y, ele é do grau 2, já que tanto no segundo, quanto no terceiro termo o grau nesta variável é dois.
O polinômio 4a2b3 + 5a5 é do grau 5 na variável a e do grau 3 em relação à variável b.
Redução de Termos Semelhantes
Assim como fizemos no caso dos monômios, também podemos fazer a redução de polinômios através da adição algébrica dos seus termos semelhantes.
No exemplo abaixo realizamos a soma algébrica do primeiro com o terceiro termo, e do segundo com o quarto termo, reduzindo um polinômio de quatro termos a um outro de apenas dois.
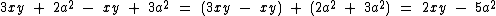
Polinômios reduzidos de dois termos também são denominados binômios. Polinômios reduzidos de três termos, também são denominados trinômios.
Veja abaixo alguns exemplos de redução de polinômios através da soma ou subtração de termos semelhantes:

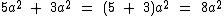

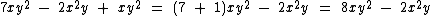

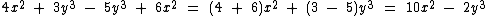

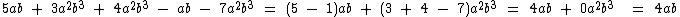
Multiplicação de Polinômios
Temos tanto o caso da multiplicação de um monômio por um polinômio, quanto o caso da multiplicação de um polinômio por um polinômio.
Multiplicação de um Polinômio por um Monômio
No primeiro caso a multiplicação é realizada multiplicando-se o monômio por cada um dos termos do polinômio.
Vejamos a multiplicação abaixo:
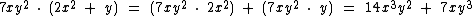
Repare que multiplicamos 7xy2 por ambos os termos do polinômio, aplicamos a propriedade distributiva da multiplicação.
Caso você ainda tenha dúvidas sobre como realizar a multiplicação de monômios, faça um revisão antes de prosseguir neste tema.
Veja mais alguns exemplos:

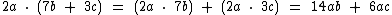

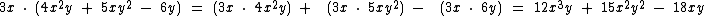

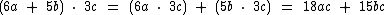

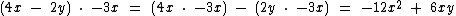
Multiplicação de um Polinômio por um Polinômio
No caso da multiplicação de polinômio por polinômio efetuamos a multiplicação de cada um dos termos do primeiro polinômio, por cada um dos termos do segundo polinômio e depois realizamos a redução do polinômio resultante.
Vamos analisar a multiplicação abaixo a qual separamos em três linhas para podermos observá-la mais facilmente:
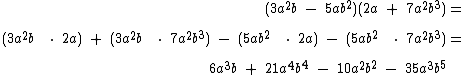
Na primeira linha temos os dois polinômios a serem multiplicados.
Os dois primeiros produtos na segunda linha foram obtidos da multiplicação de 3a2b por cada um dos dois termos do segundo polinômio, 2a e 7a2b3.
Os dois últimos produtos na segunda linha foram obtidos multiplicando-se agora o segundo termo do primeiro polinômio, também por cada um dos dois termos do segundo.
A terceira linha que é o resultado final, já que não há termos semelhantes a reduzir, é o resultado após a multiplicação dos monômios entre parênteses na linha anterior.
Analise estes outros exemplos para uma melhor assimilação:

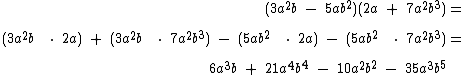

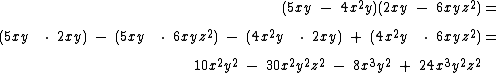

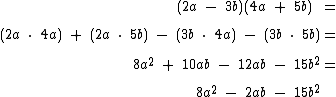

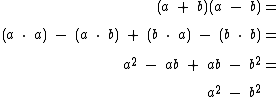
Para multiplicar mais de dois polinômios, comece multiplicando os dois primeiros, depois multiplique o polinômio obtido pelo terceiro e assim por diante até multiplicar por todos.
Para a multiplicar 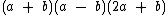 , por exemplo, primeiro multiplique
, por exemplo, primeiro multiplique 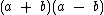 , que como vimos acima é igual a
, que como vimos acima é igual a 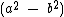 , então multiplique
, então multiplique 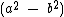 por
por 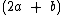 .
.
Divisão de Polinômios
Como no caso da multiplicação, temos tanto a divisão de um polinômio por um monômio, quanto a divisão de um polinômio por um polinômio. Vamos tratar cada um dos casos individualmente.
Divisão de um Polinômio por um Monômio
Este é o caso mais simples, pois podemos fazê-lo dividindo cada um dos monômios que formam o polinômio, pelo monômio em questão.
Vamos analisar a divisão do polinômio abaixo:
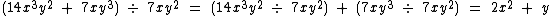
Note que desmembramos o polinômio em duas partes, dividindo tanto 14x3y2 por 7xy2, quanto 7xy3.
Em caso de dúvida consulte a divisão de monômios, que foi explicada em detalhes na página sobre este tema.
Observe mais estes exemplos:

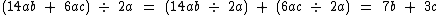

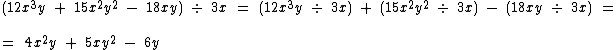

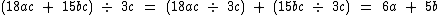

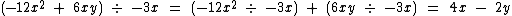

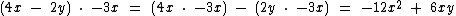
Divisão de um Polinômio por um Polinômio
Para realizarmos a divisão de polinômios é preciso que eles estejam reduzidos e ordenados.
O conceito da redução de termos semelhantes foi visto acima, quanto à ordenação de polinômios, dizemos que um polinômio está ordenado em relação à determinada variável, quando o grau de todos os monômios que os compõe, em relação a esta variável, estão ordenados de forma crescente ou decrescente.
O polinômio -5x4 + 6x5 - 7x3, não está ordenado em relação a variável x, já o polinômio 6x5 - 5x4 - 7x3 está ordenado de forma decrescente em relação a esta variável. Observe que os expoentes desta incógnita decrescem de 5 a 3.
Para explicar o procedimento da divisão de polinômios pelo método das chaves, vamos dividir 8a2 - 2ab -15b2 por 2a - 3b.
A primeira coisa a verificar é se o grau do dividendo é maior ou igual ao grau do divisor. Se for menor o quociente será zero e o resto será o próprio dividendo.
Repare que ambos os polinômios estão ordenados de forma decrescente em relação à incógnita a:
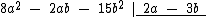
A divisão de polinômios é muito semelhante à divisão de números naturais. Vamos começar dividindo o monômio 8a2 pelo monômio 2a e colocar o quociente 4a abaixo da chave:
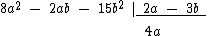
Agora vamos multiplicar por -4a, o valor oposto do quociente, cada um dos monômios do divisor 2a - 3b e colocar o resultado embaixo do dividendo:
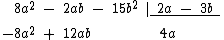
Executamos então a soma dos monômios:
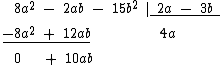
Continuamos a divisão baixando o terceiro monômio do dividendo:
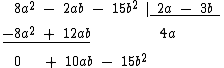
Agora dividimos 10ab por 2a, que vai dar 5b e também o colocamos abaixo da chave:
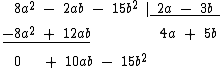
Multiplicamos por -5b, o valor oposto de 5b, cada um dos monômios do divisor 2a - 3b e colocamos o resultado embaixo do primeiro resto parcial:
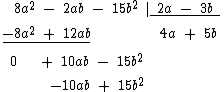
Por fim executamos a soma que resultará em zero, indicando uma divisão exata:
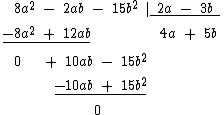
Como pudemos ver o procedimento da divisão de polinômios e bastante simples e semelhante à divisão de números naturais.
Para fechar o tema vamos a um outro exemplo, só que desta vez veremos uma divisão com um resto diferente de zero.
Vamos dividir 2x4 - 7x3 + 3x2 por x - 2:
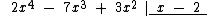
Dividimos o monômio 2x4 pelo monômio x, que resulta em 2x3 e o colocamos abaixo da chave:
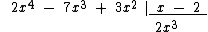
Agora vamos multiplicar por -2x3, o valor oposto do quociente, cada um dos monômios do divisor x - 2 e colocar o resultado embaixo do dividendo:
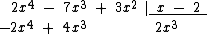
Executamos a soma dos monômios:
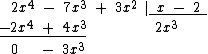
Continuamos a divisão baixando o último monômio do dividendo:
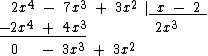
Dividimos então -3x3 por x, que vai dar -3x2 e o colocamos também abaixo da chave:
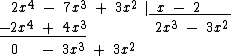
Então Multiplicamos por 3x2, que é o valor oposto de -3x2, cada um dos monômios do divisor x - 2 e colocamos o resultado embaixo do primeiro resto parcial:
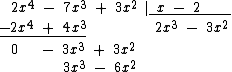
Como anteriormente, efetuamos a soma dos monômios:
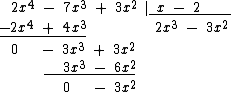
Note que o resto -3x2 é um polinômio de grau 2, que não é de grau inferior ao grau do divisor, que é um polinômio de grau 1, então devemos continuar a divisão.
Dividimos -3x2 por x e colocamos o resultado -3x abaixo da chave:
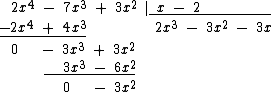
Multiplicamos por 3x, que é o simétrico de -3x, cada um dos monômios do divisor x - 2 e botamos o resultado embaixo do segundo resto parcial:
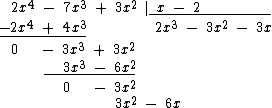
Somamos então os monômios:
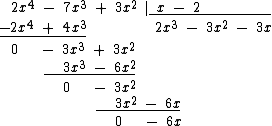
Como tanto -6x, quanto x - 2 são de grau 1, devemos continuar a divisão:
Dividimos então -6x por x, que vai dar -6 e também o inserimos abaixo da chave:
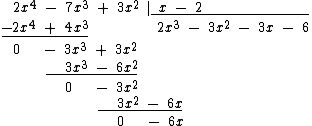
Multiplicamos por 6, que é o simétrico de -6, novamente cada um dos monômios do divisor x - 2 e botamos o resultado embaixo do terceiro resto parcial:
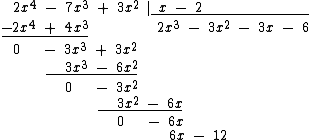
Somamos mais uma vez os monômios:
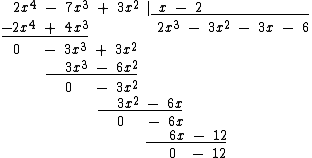
Agora o grau do resto -12 é igual a 0 e, portanto, inferior ao grau do divisor que é 1, então terminamos a divisão por aqui.
Se você realizar a multiplicação do quociente 2x3 - 3x2 - 3x - 6 por x - 2 irá obter 2x4 - 7x3 + 3x2 + 12 que somado a -12 resultará em 2x4 - 7x3 + 3x2, exatamente o dividendo original.
Para verificar se você compreendeu bem o conteúdo explicado, é desejável que você realize a multiplicação e a soma acima, para ver se consegue chegar ao mesmo resultado final. Também seria muito bom se você tentasse resolver novamente todos os exemplos resolvidos nesta página.






