Análise Combinatória - Permutação Simples
Quando estudamos o princípio fundamental da contagem tínhamos quatro livros (português, matemática, história e geografia) e calculamos o número total de formas que poderíamos empilhá-los em uma carteira escolar. Em outras palavras, fazíamos uma permutação no posicionamento destes livros na pilha sobre a carteira.
Permutação Simples
A cada um dos agrupamentos que podemos formar com certo número de elementos distintos, tal que a diferença entre um agrupamento e outro se dê apenas pela mudança de posição entre seus elementos, damos o nome de permutação simples.
Neste caso o agrupamento de livros ( português, matemática, história, geografia ), difere do agrupamento ( matemática, história, português, geografia ), pois embora os elementos de ambos os grupos sejam os mesmos, há mudança no posicionamento de ao menos um dos seus elementos.
Fórmula da Permutação Simples
Segundo o princípio fundamental da contagem vimos que o número de agrupamentos possíveis deste exemplo era dado por:
4 . 3 . 2 . 1 = 24
Na página sobre fatoriais vimos que 4 . 3 . 2 . 1 é igual a 4!, então se chamarmos de Pn a permutação simples de n elementos distintos, podemos calculá-la através da seguinte fórmula:
Pn = n!
Resolvendo o exemplo com o uso da fórmula temos:
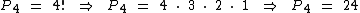
Exemplos
 Quantos anagramas podemos formar a partir da palavra ORDEM?
Quantos anagramas podemos formar a partir da palavra ORDEM?
Um anagrama é uma palavra ou frase formada com todas as letras de uma outra palavra ou frase. Normalmente as palavras ou frases resultantes são sem significado, como já era de se esperar.
Como a palavra ORDEM possui 5 letras distintas, devemos calcular o número de permutações calculando P5. Temos então:
P5 = 5! = 5 . 4 . 3 . 2 . 1 = 120
Portanto:
 O número de anagramas que podemos formar a partir da palavra ORDEM é igual 120.
O número de anagramas que podemos formar a partir da palavra ORDEM é igual 120.
 Na fila do caixa de uma padaria estão três pessoas. De quantas maneiras elas podem estar posicionadas nesta fila?
Na fila do caixa de uma padaria estão três pessoas. De quantas maneiras elas podem estar posicionadas nesta fila?
Temos que calcular P3, então:
P3 = 3! = 3 . 2 . 1 = 6
Logo:
 As três pessoas podem estar posicionas de seis maneiras diferentes na fila.
As três pessoas podem estar posicionas de seis maneiras diferentes na fila.
 Quantos são os anagramas que podemos formar a partir das letras da palavra ERVILHAS, sendo que eles comecem com a letra E e terminem com vogal?
Quantos são os anagramas que podemos formar a partir das letras da palavra ERVILHAS, sendo que eles comecem com a letra E e terminem com vogal?
Como na primeira posição sempre teremos a letra E, o número de possibilidades nesta posição é igual a 1, podemos até dizer que é igual a P1.
Para a última posição temos disponíveis as letras I e A, pois a letra E já está sendo utilizada no começo, então para a oitava letra temos que calcular P2:
P2 = 2! = 2 . 1 = 2
Como para as demais posições temos 6 letras disponíveis, calculemos então P6:
P6 = 6! = 6 . 5 . 4 . 3 . 2 . 1 = 720
Multiplicando tudo:
1 . 720 . 2 = 1440
Então:
 A partir da palavra ERVILHAS podemos formar 1440 anagramas que comecem com a letra E e terminem em vogal.
A partir da palavra ERVILHAS podemos formar 1440 anagramas que comecem com a letra E e terminem em vogal.
