Observe o triângulo retângulo ao lado:

Ele é denominado triângulo retângulo por possuir um ângulo reto, ângulo este entre a base (lado horizontal) e a altura (lado vertical).

Cada um destes lados é denominado cateto. O outro lado, o maior deles, é denominado hipotenusa.

Segundo o Teorema de Pitágoras temos que a soma do quadrado da medida dos catetos é igual ao quadrado da medida da hipotenusa, ou de forma simplificada:

A soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.

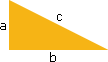
Nomeando os catetos de a e b e a hipotenusa de c, o teorema é representado pela seguinte expressão:

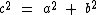
Ou ainda por:

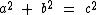
Demonstração do Teorema de Pitágoras

Teorema é qualquer proposição que precisa ser demonstrada para que seja aceita.

Há várias formas de demonstrarmos o Teorema de Pitágoras, mas aqui iremos apresentar somente uma, que além de ser fácil de se explicar, também é fácil de se entender.

Vamos tomar 4 dos triângulos acima e montar uma figura como esta ao lado:

Como podemos observar, com os quatro triângulos formamos uma figura contendo dois quadrados, um interno e outro externo.

Os lados do quadrado interno têm medida igual a c. Já a medida dos lados do quadrado externo é igual a + b.

A área do quadrado externo é igual a soma da área dos quatro triângulos mais a área do quadrado interno. Isto pode ser assim representado:

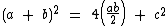
Desenvolvendo esta expressão, cujo primeiro membro é um produto notável, concluímos a prova do teorema:

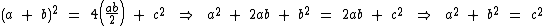
Neste nosso exemplo o cateto a é menor que o b, mas a demonstração se comprovaria mesmo que os catetos tivessem o mesmo comprimento, ou que medida de a fosse maior que a medida de b.

Exemplos da Utilização do Teorema de Pitágoras

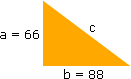
Qual é a medida da hipotenusa de um triângulo retângulo cujos catetos medem 66 cm e 88 cm?

Vamos assumir que a = 66 e que b = 88. Aplicando o teorema temos:

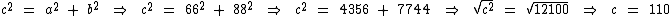
A hipotenusa mede 110 cm.

A base de um triângulo retângulo mede 48 mm e a sua hipotenusa 80 mm. Qual é a sua altura?

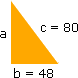
Digamos que:

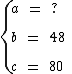
Segundo Pitágoras temos:

A altura deste triângulo é de 64 mm.

Os lados de um triângulo medem 15 m, 20 m e 23 m. Este é um triângulo retângulo?

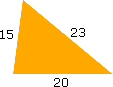
Em um triângulo retângulo a hipotenusa é sempre o maior lado, então 15 m e 20 m se referem à medida dos catetos deste suposto triângulo retângulo.

Para descobrir se temos realmente um triângulo retângulo o procedimento é simples, basta calcularmos a medida da hipotenusa, através do Teorema de Pitágoras, para verificarmos se ela mede realmente 23 m. Se medir então temos de fato um triângulo retângulo:

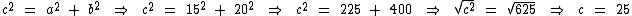
Não, este não é um triângulo retângulo. Com catetos medindo 15 m e 20 m, para que tivéssemos um triângulo retângulo a medida da hipotenusa deveria ser 25 m e não 23 m.

Dois triângulos retângulos têm em comum a altura. A medida da hipotenusa do menor é igual a 20, já a hipotenusa do maior é igual a 37. Qual é a medida das bases sabendo-se que diferença entre elas é igual a 19?

Segundo Pitágoras, para o triângulo maior temos a seguinte equação:

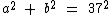
Como a diferença entre os catetos distintos é igual a 19, em relação ao triângulo menor temos:

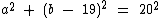
Podemos isolar a² na primeira equação:

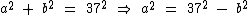
E substituí-lo na segunda:

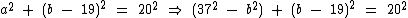
Agora vamos desenvolver a equação para obtermos a medida do cateto b:

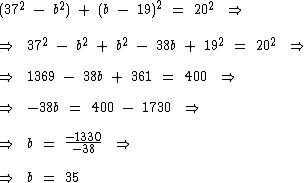
Um dos catetos mede 35 e como a diferença entre eles é igual a 19, temos que ou outro mede 16:

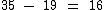
As bases medem 16 e 35.

Em relação ao problema anterior, qual é a altura dos triângulos retângulos?

Visto que os dois triângulos possuem a mesma altura, basta calcularmos a altura de apenas um deles.

Para trabalharmos com números menores vamos calcular utilizando os dados do triângulo menor:

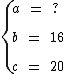
Basta aplicarmos Teorema de Pitágoras:

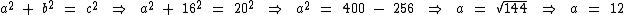
A altura dos triângulos retângulos é igual 12.

Teorema de Pitágoras e os Números Irracionais.

Nos casos mostrados até aqui neste artigo, tivemos o cuidado de escolher triângulos com todos os lados sendo representados por números naturais. A intenção disto era facilitar o entendimento da matéria. Na prática porém, na maioria das vezes, principalmente a hipotenusa será um número irracional.

Quando isolamos uma das variáveis em função das outras, temos os seguintes casos:

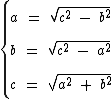
Nestes casos, quando o radicando não for um quadrado perfeito, a variável isolada será um número irracional.

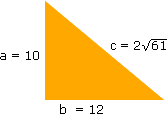
Observe o triângulo retângulo ao lado:

Veja que a medida da sua hipotenusa é um número irracional.

Vamos calculá-la em função da medida dos catetos:

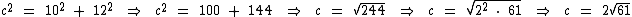
é um número irracional, pois não existe nenhum número natural que multiplicado por ele próprio resulte em 61.