Análise Combinatória - Princípio Fundamental da Contagem
Em uma carteira escolar temos quatro livros de diferentes matérias, empilhados de cima para baixo nesta exata ordem:
Português, matemática, história e geografia.
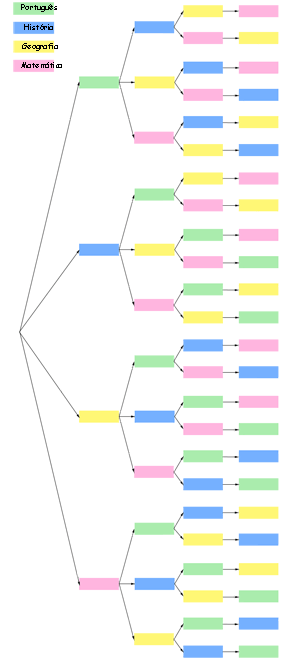
Incluindo a ordem atual, de quantas maneiras no total podemos empilhar tais livros nesta carteira?
Vamos pensar sobre o problema.
Na escolha do primeiro livro a ser colocado na carteira temos 4 possibilidades, pois ainda não colocamos nenhum livro nela, temos então quatro livros a escolher: Português, matemática, história e geografia.
Se começarmos a pilha com o livro de português, na escolha do próximo livro a ser colocado sobre ele, temos 3 possibilidades: matemática, história e geografia.
Se escolhermos o livro de história como o segundo livro da pilha, para o terceiro livro temos 2 possibilidades apenas: matemática e geografia.
Se colocarmos na pilha o livro de geografia, para o último livro temos obviamente 1 possibilidade: matemática.
Veja pela figura ao lado que as 4 possibilidades do primeiro livro podem ser combinadas com cada uma das 3 possibilidades do segundo livro, que podem ser combinadas com cada uma das 2 possibilidades do terceiro livro, que podem finalmente ser combinadas com 1 possibilidade do quarto livro. Matematicamente o número total de possibilidades seria:
4 . 3 . 2 . 1 = 24
Neste cálculo utilizamos o princípio fundamental da contagem.
Princípio Fundamental da Contagem
O princípio fundamental da contagem diz que um evento que ocorre em n situações independentes e sucessivas, tendo a primeira situação ocorrendo de m1 maneiras, a segunda situação ocorrendo de m2 maneiras e assim sucessivamente até a n-ésima situação ocorrendo de mn maneiras, temos que o número total de ocorrências será dado pelo produto:

Exemplos
 Quantos são os números naturais de dois algarismos que são múltiplos de 5?
Quantos são os números naturais de dois algarismos que são múltiplos de 5?
Como o zero à esquerda de um número não é significativo, para que tenhamos um número natural com dois algarismos ele deve começar com um dígito de 1 a 9, temos portanto 9 possibilidades.
Para que o número seja um múltiplo de 5, o mesmo deve terminar em 0 ou 5, portanto temos apenas 2 possibilidades.
A multiplicação de 9 por 2 nos dará o resultado desejado.
Logo:
 São 18 os números naturais de dois algarismos que são múltiplos de 5.
São 18 os números naturais de dois algarismos que são múltiplos de 5.
 Eu possuo 4 pares de sapatos e 10 pares de meias. De quantas maneiras poderei me calçar utilizando um par de meias e um de sapatos?
Eu possuo 4 pares de sapatos e 10 pares de meias. De quantas maneiras poderei me calçar utilizando um par de meias e um de sapatos?
Pelo princípio fundamental da contagem temos que multiplicar 4, que é o número de elementos do primeiro conjunto, por 10 que corresponde ao número de elementos do segundo conjunto.
Portanto:
 Poderei me calçar de 40 maneiras diferentes.
Poderei me calçar de 40 maneiras diferentes.
 De quantas formas podemos dispor as letras da palavra FLUOR de sorte que a última letra seja sempre a letra R?
De quantas formas podemos dispor as letras da palavra FLUOR de sorte que a última letra seja sempre a letra R?
Para a última letra, segundo o enunciado temos apenas uma possibilidade que é a letra R.
Para a primeira, segunda, terceira e quarta letras temos respectivamente 4, 3, 2 e 1 possibilidades. Assim temos:
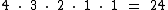
Note que este exemplo é semelhante ao caso dos livros, explicado no início da página, só que neste caso teríamos mais um livro, digamos de ciências, que sempre seria colocado na pilha por último.
 Podemos dispor as letras da palavra FLUOR de 24 formas diferentes, tal que a última letra seja sempre a letra R.
Podemos dispor as letras da palavra FLUOR de 24 formas diferentes, tal que a última letra seja sempre a letra R.
 Quantos números naturais com 3 algarismos podemos formar que não comecem com 16, nem com 17?
Quantos números naturais com 3 algarismos podemos formar que não comecem com 16, nem com 17?
Neste exemplo iremos fazer o cálculo em duas partes. Primeiro iremos calcular quantos são os números com três algarismos.
Como neste caso na primeira posição não podemos ter o dígito zero, o número de possibilidades para cada posição é respectivamente: 9, 10 e 10.
Portanto temos 900 números naturais com três dígitos.
Agora vamos calcular quantos deles começam com 16 ou 17.
Para a primeira posição temos apenas uma possibilidade, o dígito 1. Para a segunda temos 2, pois servem tanto o dígito 6, quanto o 7.
Para a terceira e última posição temos todos os dígitos possíveis, ou seja, 10 possibilidades.
Multiplicando tudo temos 20.
Logo, subtraindo 20 de 900 obtemos 880.
 Existem 880 números naturais nestas condições.
Existem 880 números naturais nestas condições.
 São quantos os números ímpares com três algarismos, que não possuem dígitos repetidos e que de trás para frente também são ímpares?
São quantos os números ímpares com três algarismos, que não possuem dígitos repetidos e que de trás para frente também são ímpares?
Os números devem ser ímpares, temos então 5 possibilidades para o último algarismo.
A história do "de trás para frente", em outras palavras quer dizer que o primeiro algarismo também é ímpar. Como um dígito ímpar já foi utilizado na última posição, temos então apenas 4 disponíveis para a primeira posição.
Para o dígito central temos apenas 8 possibilidades, pois dois dígitos ímpares já foram utilizados.
Multiplicando 4 por 8 e por 5 obtemos 160.
Assim sendo:
 São 160 os números ímpares que satisfazem a todas estas condições.
São 160 os números ímpares que satisfazem a todas estas condições.
