Resolução Passo a Passo de Questões de Concursos Públicos - I
Grande parte dos estudantes que acessam o Matemática Didática são pessoas interessadas em prestar concursos públicos, por isto decidimos criar um grupo de páginas envolvendo questões de vários destes concursos.
Nestas páginas você encontrará questões de várias instituições do país.
Em conformidade com o estilo de ensino do Matemática Didática, as questões serão resolvidas em detalhes, para que os estudantes que as analisem, possam resolver outras questões semelhantes, seja pelo entendimento dos conceitos aplicados, seja simplesmente por analogia.
Cada uma das páginas conterá dez questões sobre conceitos diversos, não se atendo a um único tema como ocorre nas demais páginas de exercícios do site.
Estas páginas também irão diferir das páginas dos simulados do Matemática Didática e dos próprios concursos em si, pois para cada questão teremos apenas o enunciado, a resolução e a resposta. Não teremos as opções de múltipla escolha.
Muitas das resoluções irão se referir a temas ainda não tratados no site, mas ainda assim será possível compreendê-las. Os temas que já foram aqui tratados irão conter links para as referidas páginas.
Nossa intenção é apenas mostrar uma forma de resolver as questões. Se um problema envolve a resolução de uma equação do segundo grau, por exemplo, nosso foco não será ensinar como resolver equações deste tipo, mas sim como solucionar o problema em si.
Esta página contém a resolução das dez primeiras questões publicadas. Aos poucos iremos publicando mais e mais questões resolvidas.
Bons estudos e boa sorte em seus concursos!
 1) Uma pessoa caminha em uma pista plana com a forma de triângulo retângulo. Ao dar uma volta completa na pista com velocidade constante de caminhada, ela percorre 600 e 800 metros nos trajetos correspondentes aos catetos da pista triangular, e o restante da caminhada ela completa em 10 minutos. A velocidade constante de caminhada dessa pessoa é igual a quantos quilômetros por hora?
1) Uma pessoa caminha em uma pista plana com a forma de triângulo retângulo. Ao dar uma volta completa na pista com velocidade constante de caminhada, ela percorre 600 e 800 metros nos trajetos correspondentes aos catetos da pista triangular, e o restante da caminhada ela completa em 10 minutos. A velocidade constante de caminhada dessa pessoa é igual a quantos quilômetros por hora?
A resolução desta questão se baseia no teorema de Pitágoras. Vamos descobrir a medida do trajeto percorrido em 10 minutos, a partir do qual iremos calcular a velocidade procurada.
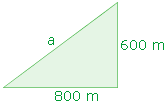
Para solucionar o problema vamos observar a figura ao lado que representa a pista em questão.
Em função do enunciado sabemos que o lado a, correspondente à hipotenusa, foi percorrido em 10 minutos, assim sendo, basta descobrirmos o seu comprimento para podermos calcular a velocidade na qual ele foi percorrido, que é constante em todo o percurso.
Segundo o teorema de Pitágoras o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos, para quaisquer triângulos retângulos.
O teorema pode ser representado pela seguinte equação:
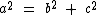
Neste nosso problema temos b = 600 e c = 800, o que nos leva à seguinte equação:
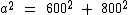
Agora temos condições de descobrir quantos metros possui o trecho da pista que foi percorrido em dez minutos.
Vejamos:
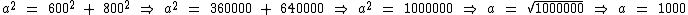
Agora sabemos o trecho percorrido em dez minutos tem 1000 m de comprimento.
Se em 10 min percorremos 1000 m, em 60 min (ou seja, em 1 h) vamos percorrer quantos metros?
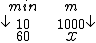
Resolvendo a regra de três simples e direta temos:
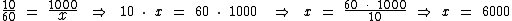
Então a velocidade constante de caminhada foi de 6000 m por hora, mas o enunciado pede a velocidade em km/h, por isto precisamos realizar mais uma conversão, agora de m para km.
Já aprendemos que a conversão de metros para quilômetros é realizada dividindo-se por 1000 a medida em metros. Como temos 6000 metros, ao dividi-los por 1000 obtemos 6 quilômetros.
Portanto:
 A velocidade constante de caminhada é de 6 km/h.
A velocidade constante de caminhada é de 6 km/h.
 2) Um professor aplicou duas provas, cada uma valendo 10. O combinado com seus alunos era que a média final de cada um seria calculada utilizando-se peso 1 na nota da primeira prova e peso 2 na nota da segunda prova. Na hora de fazer os cálculos da média de um aluno, o professor trocou os pesos entre as duas provas, obtendo média igual a 5. Corrigido o erro, a média do aluno subiu 1 ponto. Nas condições do problema, a nota que esse aluno tirou na segunda prova superou sua nota da primeira prova em quantos por cento?
2) Um professor aplicou duas provas, cada uma valendo 10. O combinado com seus alunos era que a média final de cada um seria calculada utilizando-se peso 1 na nota da primeira prova e peso 2 na nota da segunda prova. Na hora de fazer os cálculos da média de um aluno, o professor trocou os pesos entre as duas provas, obtendo média igual a 5. Corrigido o erro, a média do aluno subiu 1 ponto. Nas condições do problema, a nota que esse aluno tirou na segunda prova superou sua nota da primeira prova em quantos por cento?
A resolução desta outra questão envolve tanto o cálculo da média aritmética ponderada, quanto o cálculo de porcentagem.
Em resumo precisamos descobrir o valor de cada nota, para então descobrimos quantos por cento a segunda nota é maior que a primeira. Vamos então à resolução.
Segundo o enunciado, erroneamente a média foi calculada com os pesos invertidos. A primeira nota tendo peso 2 e a segunda peso 1:
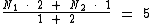
No entanto a média deveria ser calculada tendo a primeira nota peso 1 e a segunda peso 2:
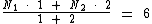
Note que com os pesos corretos a média passou de 5 a 6 conforme o enunciado.
Vamos tratar as equações eliminado assim as frações:
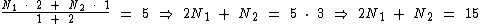
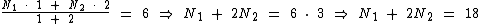
Como temos duas variáveis com duas equações, vamos montar um sistema de equações com duas variáveis para identificarmos o valor de cada nota obtida pelo aluno:
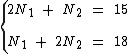
Vamos eliminar N2 multiplicando a primeira equação por -2 e somando à segunda equação, obtendo assim o valor de N1:
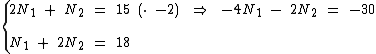
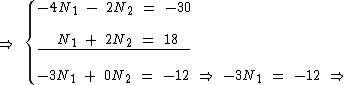
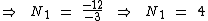
Agora podemos obter o valor de N2 substituindo N1 pelo seu valor na primeira equação:
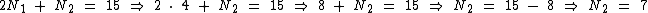
Agora sabemos que o aluno teve nota 4 na primeira prova e nota 7 na segunda prova.
Como o enunciado pergunta quantos por cento a segunda nota é maior que a primeira, precisamos dividir a diferença entre a segunda e a primeira, pela primeira nota:
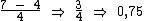
Esta divisão resulta em 0,75 que é o valor procurado, mas na forma decimal, precisamos então multiplicá-lo por 100% para convertê-lo na forma percentual:
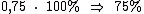
Então:
 A nota que esse aluno tirou na segunda prova superou sua nota da primeira prova em 75%.
A nota que esse aluno tirou na segunda prova superou sua nota da primeira prova em 75%.
 3) Bel, Karen e Isabella são três embarcações que navegam, respectivamente, com velocidades de 40 km/h, 50 km/h e 60 km/h. Bel começou sua viagem às 7 h e Karen, às 9 h. Sabe-se que as três embarcações partiram de um mesmo local e seguiram a mesma rota. Para que todas se encontrem num mesmo horário, qual deve ser o horário em que Isabella começou a sua viagem?
3) Bel, Karen e Isabella são três embarcações que navegam, respectivamente, com velocidades de 40 km/h, 50 km/h e 60 km/h. Bel começou sua viagem às 7 h e Karen, às 9 h. Sabe-se que as três embarcações partiram de um mesmo local e seguiram a mesma rota. Para que todas se encontrem num mesmo horário, qual deve ser o horário em que Isabella começou a sua viagem?
Este problema requer que calculemos a que distância do ponto de partida estarão Bel e Karen quando se encontrarem, sendo que Bel, que é a mais lenta das três embarcações, partiu 2 horas mais cedo e depois calculemos quanto tempo Isabella gasta para fazer tal percurso, a fim de calcularmos a que horas ela deve partir.
A distância percorrida pode ser obtida multiplicando-se a velocidade pelo tempo de viagem. Sabendo disto, podemos montar a seguinte equação a partir dos dados fornecidos pelo enunciado:
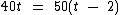
No primeiro membro desta equação estamos calculando a distância percorrida por Bel, já no segundo membro calculamos a distância percorrida por Karen. Sendo t a variável que indica o tempo no percurso em horas, note que Karen tem duas horas a menos de viagem, pois partiu duas horas mais tarde.
Solucionando esta equação do primeiro grau iremos descobrir que as duas primeiras embarcações que partiram se encontraram dez horas depois da partida da primeira:
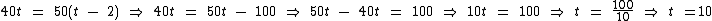
Às 17 h tanto Bel quanto Karen estavam no mesmo ponto após terem percorrido 400 km (o produto de 40 km/h por 10 h referente a Bel, ou de 50 km/h por 8 h referente a Karen). Então precisamos calcular em quanto tempo Isabella consegue fazer tal percurso na velocidade de 60 km/h. Obtemos tal tempo dividindo 400 km por 60 km/h:
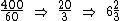
Agora sabemos que Isabella demora 6 h e mais 2/3 h para fazer tal percurso. Vamos então subtrair este número de horas de 17 h que é o horário no qual as três embarcações devem se encontrar:
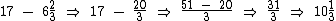
Isabella deve partir às 10 1/3 h.
Para convertemos 1/3 h em minutos vamos multiplicá-lo por 60 min/h, já que temos sessenta minutos em uma hora:
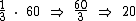
Logo:
 Isabella começou a sua viagem às 10h 20min.
Isabella começou a sua viagem às 10h 20min.
 4) Os vídeos são exibidos, em uma televisão, usualmente a 30 quadros por segundo, uma velocidade que proporciona uma sensação natural de movimento. Para mostrar detalhes de movimentos muito rápidos, algumas câmeras conseguem filmar a uma taxa de 324 000 quadros por segundo. Se o número de quadros filmados com essas câmeras, durante um segundo, fosse exibido na velocidade usual, qual seria a duração do vídeo em horas?
4) Os vídeos são exibidos, em uma televisão, usualmente a 30 quadros por segundo, uma velocidade que proporciona uma sensação natural de movimento. Para mostrar detalhes de movimentos muito rápidos, algumas câmeras conseguem filmar a uma taxa de 324 000 quadros por segundo. Se o número de quadros filmados com essas câmeras, durante um segundo, fosse exibido na velocidade usual, qual seria a duração do vídeo em horas?
Neste caso não há muito que pensar. Se 324000 quadros são exibidos em um segundo na alta velocidade e apenas 30 quadros na velocidade usual, ao dividirmos 324000 por 30 iremos encontrar o número de segundos que durará a exibição do vídeo:
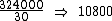
Como é solicitada a resposta em horas, precisamos fazer a conversão.
Já que em 1 h temos 60 min e em 1 min temos 60 seg, então temos 3600 seg em 1 h:
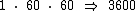
Para transformarmos os 10800 seg em horas vamos dividi-los por 3600 seg/h:
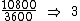
Portanto:
 A duração do vídeo na velocidade usual de 30 quadros por segundo seria de 3 horas.
A duração do vídeo na velocidade usual de 30 quadros por segundo seria de 3 horas.
 5) Hoje, a idade de um pai é o quíntuplo da idade de seu filho e, daqui a 15 anos, a soma das idades será de 60 anos. Pode-se afirmar que daqui a 15 anos, a idade do pai será quantas vezes a idade do filho?
5) Hoje, a idade de um pai é o quíntuplo da idade de seu filho e, daqui a 15 anos, a soma das idades será de 60 anos. Pode-se afirmar que daqui a 15 anos, a idade do pai será quantas vezes a idade do filho?
Nesta questão iremos montar um sistema de equações do primeiro grau com duas incógnitas para obtermos a idade do pai e a idade do filho, depois iremos utilizar o conceito de razão para descobrirmos quantas vezes a primeira é maior que a última.
A idade do pai é o quíntuplo da idade do seu filho, o que nos leva à seguinte equação:
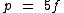
Onde p é a idade do pai e f a idade do filho.
Daqui a 15 anos a soma das idades será de 60 anos. Isto pode ser expresso como:
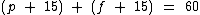
Para ficar mais simples o trabalho, vamos simplificar a expressão:
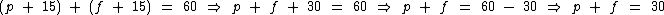
Vamos então montar o sistema de equações:
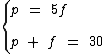
Vamos solucioná-lo pelo método da substituição. Na segunda equação vamos substituir p por 5f:
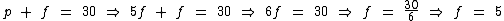
Agora podemos substituir f por 5 na primeira equação:
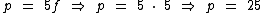
Sabendo que o pai tem 25 anos e que o filho tem 5 anos, basta calcularmos a razão das idades que eles terão daqui quinze anos:
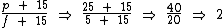
Então:
 Daqui a 15 anos, a idade do pai será 2 vezes a idade do filho.
Daqui a 15 anos, a idade do pai será 2 vezes a idade do filho.
 6) Em uma determinada turma, a razão entre o número de meninas e o número de meninos, nessa ordem, é igual a 1/3 e, em outra turma, com o mesmo número de alunos, essa razão é 3/2. Quando juntaram as duas turmas para assistir a um filme, os professores das duas turmas perceberam que a razão entre o número de meninas e o número de meninos, nessa ordem, passou a ser igual a quanto?
6) Em uma determinada turma, a razão entre o número de meninas e o número de meninos, nessa ordem, é igual a 1/3 e, em outra turma, com o mesmo número de alunos, essa razão é 3/2. Quando juntaram as duas turmas para assistir a um filme, os professores das duas turmas perceberam que a razão entre o número de meninas e o número de meninos, nessa ordem, passou a ser igual a quanto?
Esta questão tem como resposta a razão entre o número total de meninas e o número total de meninos. A dificuldade é que não se conhece o número de alunos em cada classe. Sabe-se, porém que elas têm o mesmo número de alunos no total.
Como número de meninas para o número de meninos na primeira classe está na razão de 1 para 3, podemos dizer que o número total de alunos desta classe pode ser dividido em 4 partes iguais, sendo 1 parte composta de meninas e 3 partes contendo apenas meninos. Chamando de C1 cada uma desta partes, podemos escrever a seguinte expressão:
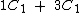
De forma análoga, o número de meninas para o número de meninos na segunda classe está na razão de 3 para 2, então o número total de alunos desta classe pode ser dividido em 5 partes iguais, das quais 3 partes contendo somente meninas e 2 partes contendo apenas meninos. Chamando de C2 estas partes individuais, temos então a expressão:
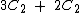
Como o número de alunos nas duas classes é o mesmo, podemos expressar este fato pela seguinte equação:
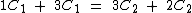
Agora vamos isolar C1:
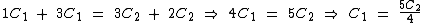
O número total de meninas juntando-se as duas classes é dado por 1C1 + 3C2, sendo uma parte vinda da primeira classe e três partes vindas da segunda classe.
Já para os meninos, vieram três partes da primeira classe e duas partes da segunda, então o número total de meninos é igual a 3C1 + 2C2.
A razão entre estas duas expressões é a razão que estamos procurando:
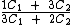
Precisamos eliminar tanto C1 quanto C2. Para isto vamos lembrar que:
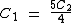
Substituindo C1 pelo seu equivalente na expressão anterior, temos:
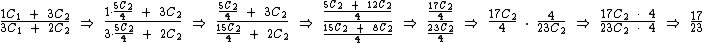
Logo:
 Quando juntaram as duas turmas os professores perceberam que a razão entre o número de meninas e o número de meninos passou a ser igual 17/23.
Quando juntaram as duas turmas os professores perceberam que a razão entre o número de meninas e o número de meninos passou a ser igual 17/23.
 7) Suponha que o preço da ação de uma empresa tenha sofrido as seguintes variações sucessivas no primeiro trimestre de um determinado ano: em janeiro, aumentou 12%; em fevereiro, sofreu uma redução de 8%; e, em março, uma redução de 4%, sempre em relação ao mês anterior. Considerando-se essas variações, ao final do trimestre, em relação ao preço original, o preço da ação subiu ou desceu quanto por cento aproximadamente (sem casas decimais)?
7) Suponha que o preço da ação de uma empresa tenha sofrido as seguintes variações sucessivas no primeiro trimestre de um determinado ano: em janeiro, aumentou 12%; em fevereiro, sofreu uma redução de 8%; e, em março, uma redução de 4%, sempre em relação ao mês anterior. Considerando-se essas variações, ao final do trimestre, em relação ao preço original, o preço da ação subiu ou desceu quanto por cento aproximadamente (sem casas decimais)?
Resolvemos esta questão através do cálculo em sequência de porcentagens.
Quando queremos acrescentar 12% a um valor, devemos multiplicá-lo por 1,12:
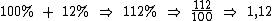
O 100% se refere ao valor original e o 12% se refere ao acréscimo.
Para reduzirmos 8% precisamos multiplicar por 0,92:
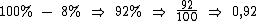
A redução de 4% é realizada da mesma forma multiplicando por 0,96:
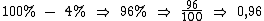
Multiplicando estes três percentuais na forma decimal iremos descobrir se o valor da ação aumentou, diminui, ou se manteve o mesmo:
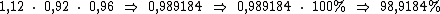
Como 98,9184% é inferior a 100%, isto indica que o valor da ação diminui.
Obtemos a variação percentual calculando a diferença:
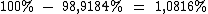
Portanto:
 O preço da ação desceu aproximadamente 1%.
O preço da ação desceu aproximadamente 1%.
 8) A razão entre os números (x+3) e 7 é igual à razão entre os números (x-3) e 5. Nessas condições, o valor de x é?
8) A razão entre os números (x+3) e 7 é igual à razão entre os números (x-3) e 5. Nessas condições, o valor de x é?
 9) Um cozinheiro dispõe de 10 litros de uma mistura de água e leite em quantidades iguais. Para obter uma mistura com 2/5 de água e 3/5 de leite, ele deve acrescentar aos 10 litros da mistura quantos litros do que?
9) Um cozinheiro dispõe de 10 litros de uma mistura de água e leite em quantidades iguais. Para obter uma mistura com 2/5 de água e 3/5 de leite, ele deve acrescentar aos 10 litros da mistura quantos litros do que?
Quando temos um todo e precisamos obter a parte referente a uma fração do mesmo, multiplicamos o todo por tal fração. Na resolução desta questão vamos fazer o cálculo inverso.
Originalmente tínhamos o mesmo volume dos líquidos, isto é, 5 l de água e 5 l de leite. Pretendemos ficar com a proporção de 2/5 de água e 3/5 de leite. De onde concluímos que devemos aumentar a quantidade de leite, pois a proporção de leite será maior.
Como a quantidade de água não aumentou, isto quer dizer que os 5 l de água originais representarão 2/5 do novo volume final.
Entendido isto se pode dizer que o problema está resolvido.
Se tivéssemos o novo volume total, para calcularmos quanto daria 2/5 dele, o multiplicaríamos por esta fração e iríamos obter 5 l. Como temos os 5 l, precisamos fazer o cálculo inverso, isto é, dividirmos 5 l por 2/5 para obtermos o novo volume total:
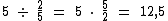
Como tínhamos originalmente 10 l e iremos ficar com 12,5 l após o acréscimo do leite, isto quer dizer que acrescentamos 2,5 l de leite:
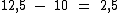
Logo:
 O cozinheiro deve acrescentar 2,5 litros de leite.
O cozinheiro deve acrescentar 2,5 litros de leite.
 10) Um artesão produz colares formados por 60 pedras divididas entre ametistas, a um custo de R$ 0,50 a pedra, e jades, a R$ 1,00 a pedra. Para baratear o preço de cada colar, o artesão aumentou a quantidade de ametistas em 4 pedras e diminuiu a de jades em 4 pedras, obtendo o preço de R$ 40,00 o colar. Qual o preço original de cada colar?
10) Um artesão produz colares formados por 60 pedras divididas entre ametistas, a um custo de R$ 0,50 a pedra, e jades, a R$ 1,00 a pedra. Para baratear o preço de cada colar, o artesão aumentou a quantidade de ametistas em 4 pedras e diminuiu a de jades em 4 pedras, obtendo o preço de R$ 40,00 o colar. Qual o preço original de cada colar?
Nesta questão temos um outro sistema de equações do primeiro grau com duas incógnitas conforme podemos observar no enunciado.
Vamos representar por a a variável referente às ametistas e por j a incógnitas referentes às jades.
O artesão produz colares contendo ametistas e jades em um total de 60 pedras:
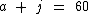
Além disto sabemos que cada pedra de jade custa R$ 1,00 e que cada pedra de ametista custa R$ 0,50.
Sabemos também que um colar com 60 pedras sai por R$ 40,00 se tiver 4 pedras de ametista a mais e 4 pedras de jade a menos que o colar padrão:
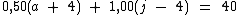
Esta expressão pode ser simplificada:
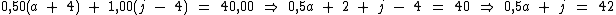
Podemos então montar o seguinte sistema:
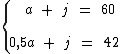
Subtraindo a segunda equação da primeira temos:
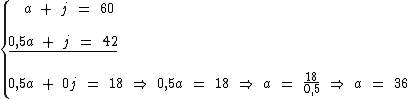
Como a = 36, podemos substituí-lo na primeira equação para encontramos o valor de j:
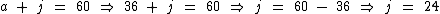
Temos um total de R$ 18,00 em ametistas, pois temos 36 pedras ao custo unitário de R$ 0,50:
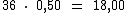
Em jade temos R$ 24,00 pois temos 24 pedras que custam R$ 1,00 a unidade:
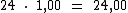
Então o colar original custa R$ 42,00:
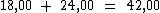
Portanto:
 O preço original de cada colar é R$ 42,00.
O preço original de cada colar é R$ 42,00.







