Em uma família com 4 integrantes, o primeiro consome 1200 ml de leite por dia, o segundo 1400 ml, o terceiro 1000 ml e o quarto integrante consome 1600 ml de leite por dia.

O consumo total diario desta família também seria de 5200 ml se cada um dos seus 4 integrantes consumisse 1300 ml diarios de leite.

A função da média é justamente esta, transformar um conjunto de números diversos em um único valor, a fim de que se possa ter uma visão global sobre os dados.

Média Aritmética Simples

Dos vários tipos de médias utilizados, o mais simples e o mais comum é a média aritmética simples.

Dados os números 1200, 1400, 1000 e 1600, para apurarmos o valor médio artimético deste conjunto, simplesmente o totalizamos e dividimos o total obtido pela quantidade de valores do conjunto:

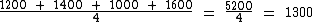
Agora preste atenção neste conjunto de números após o colocarmos em ordem crescente:

{ 1000, 1200, 1400, 1600 }

Observe que se fossemos inserir o valor médio de 1300 neste conjunto de números ordenados, a sua posição seria exatamente no meio da sequência, ou seja, seria o valor médio.

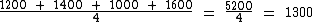
Observe ainda está propriedades das médias, que se o valor médio for inserido ao conjunto de números originais, a média ainda continuará a mesma:

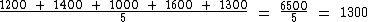
Digamos que em um concurso você tenha feito três provas e tenha tirado as seguintes notas: 10, 8 e 3. Qual foi a sua nota média afinal?

Vejamos:

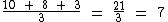
Como a nota mínima para passar no concurso era a nota 7, você se sente feliz e aliviado por ter conseguido alcançá-la.

Média Aritmética Ponderada

Mas foi aí que lhe veio a surpresa! Na última hora você soube que a nota média seria calculada atribuindo-se um peso diferente a cada prova. Você fica apreensivo. E agora?!?

Nos bastidores você soube que a primeira prova teria peso 3, a segunda peso 2 e a terceira teria peso 5. Vamos aos cálculos:

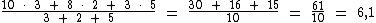
Que pena meu rapaz! Infelizmente a sua média de 6,1 não atingiu o valor mínimo de 7.

Epa! Espere um pouco! Você cometeu um erro! Os pesos não estão na ordem correta! A primeira prova teria peso 3, a segunda peso 5 e a terceira teria peso 2. Vejamos se houve alguma mudança, parece-me que você ainda tem chances:

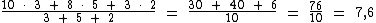
Parabéns! Você foi aprovado, afinal de contas a sua média final até melhorou!

Como você pode perceber, a média aritmética ponderada possibilita atribuir peso ou importância diferentes a cada valor. Provavelmente por ser mais importante no processo de seleção, a segunda nota tinha um peso maior. Por isto os itens com maior peso influenciam mais na média final que os de menor peso. Veja o exemplo abaixo:

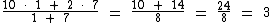
Você percebe que o primeiro valor tem peso 1, sete vezes menor que o peso do segundo valor que é igual a 7. Por isto a média final se aproximou muito mais de segundo valor (2), que do primeiro (10), embora este tenha sido cinco vezes maior que o segundo.

Resumindo, para se apurar a média aritmética ponderada, primeiramente multiplique cada valor pelo seu respectivo peso. Some todos os produtos encontrados e divida este total pela soma dos pesos.