Exercícios resolvidos - Média Aritmética Simples e Ponderada e Média Geométrica
Para maiores informações teóricas sobre este assunto veja também:Média Aritmética Simples e Ponderada
 1) Qual é a média aritmética simples dos números 11, 7, 13 e 9?
1) Qual é a média aritmética simples dos números 11, 7, 13 e 9?
Como visto na parte teórica, a solução deste exercício resume-se em somarmos os números e dividirmos este total por quatro, que é a quantidade de números:
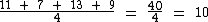
Logo:
 A média aritmética simples destes números é 10.
A média aritmética simples destes números é 10.
 2) Qual é a média aritmética ponderada dos números 10, 14, 18 e 30 sabendo-se que os seus pesos são respectivamente 1, 2, 3 e 5?
2) Qual é a média aritmética ponderada dos números 10, 14, 18 e 30 sabendo-se que os seus pesos são respectivamente 1, 2, 3 e 5?
Neste outro caso a solução consiste em multiplicarmos cada número pelo seu respectivo peso e somarmos todos estes produtos. Este total deve ser então dividido pela soma total dos pesos:
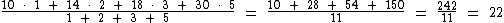
Assim sendo:
 A média aritmética ponderada deste conjunto de números é 22.
A média aritmética ponderada deste conjunto de números é 22.
 3) Qual é a média geométrica dos números 2, 4, 8, 16 e 32?
3) Qual é a média geométrica dos números 2, 4, 8, 16 e 32?
Se dispusermos de uma calculadora científica, este exercício pode ser solucionado multiplicando-se todos os números e extraindo-se do produto final, a raiz de índice cinco, pois se tratam de cinco números:
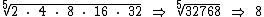
Se não dispusermos de uma calculadora científica esta solução ficaria meio inviável, pois como iríamos extrair tal raiz, isto sem contar na dificuldade em realizarmos as multiplicações?
Repare que todos os números são potência de 2, podemos então escrever:
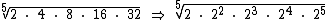
Como dentro do radical temos um produto de potências de mesma base, somando-se os expoentes temos:
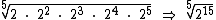
Finalmente dividindo-se o índice e o expoente por 5 e resolvendo a potência resultante:
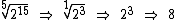
Então:
 A média geométrica deste conjunto de números é 8.
A média geométrica deste conjunto de números é 8.
 4) Dado um conjunto de quatro números cuja média aritmética simples é 2,5 se incluirmos o número 8 neste conjunto, quanto passará a ser a nova média aritmética simples?
4) Dado um conjunto de quatro números cuja média aritmética simples é 2,5 se incluirmos o número 8 neste conjunto, quanto passará a ser a nova média aritmética simples?
Na parte teórica vimos que a soma dos elementos de um conjunto de números, dividida pela quantidade de elementos deste conjunto, resulta na média aritmética simples entre eles. Se chamarmos esta soma de S, em função do enunciado podemos nos expressar matematicamente assim:
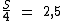
Passando o divisor 4 para o segundo membro e o multiplicando pelo termo 2,5, obteremos a soma destes quatro números que é igual a 10:
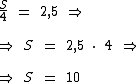
Ao incluirmos o número 8 neste conjunto de números, a soma dos mesmos passará de 10 para 18 e como agora teremos 5 números ao invés de 4, a média dos mesmos será 18 dividido por 5 que é igual a 3,6:
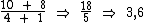
Portanto:
 Ao inserirmos o número 8 neste conjunto de números, a média aritmética simples passará a ser igual a 3,6.
Ao inserirmos o número 8 neste conjunto de números, a média aritmética simples passará a ser igual a 3,6.
 5) Em uma sala de aula os alunos têm altura desde 130cm até 163cm, cuja média aritmética simples é de 150cm. Oito destes alunos possuem exatamente 163cm. Se estes oito alunos forem retirados desta classe, a nova média aritmética será de 148cm. Quantos alunos há nesta sala de aula?
5) Em uma sala de aula os alunos têm altura desde 130cm até 163cm, cuja média aritmética simples é de 150cm. Oito destes alunos possuem exatamente 163cm. Se estes oito alunos forem retirados desta classe, a nova média aritmética será de 148cm. Quantos alunos há nesta sala de aula?
Sabemos que a média aritmética simples de um conjunto de números é igual à soma dos mesmos dividida pela quantidade de números deste conjunto. Se chamarmos de S a soma da altura de todos os alunos desta classe e de n o número total de alunos, podemos escrever a seguinte equação:
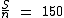
Isolando a variável S temos:

O enunciado nos diz que se retirarmos todos os oito alunos que medem 163cm, teremos 148cm como a nova média de altura da turma. Expressando esta informação em forma de equação temos:
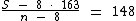
Novamente isolemos a variável S:
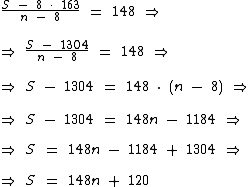
Como na primeira equação calculamos que  , vamos trocar S na segunda equação por 150n:
, vamos trocar S na segunda equação por 150n:
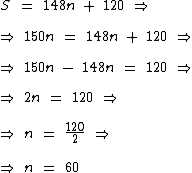
Enfim:
 Nesta sala de aula há 60 alunos.
Nesta sala de aula há 60 alunos.
 6) Dados dois números quaisquer, a média aritmética simples e a média geométrica deles são respectivamente 20,5 e 20. Quais são estes dois números?
6) Dados dois números quaisquer, a média aritmética simples e a média geométrica deles são respectivamente 20,5 e 20. Quais são estes dois números?
Chamemos de a e b estes dois números.
A média aritmética deles pode ser expressa como:
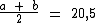
Já média geométrica pode ser expressa como:
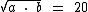
Vamos isolar a na primeira equação:
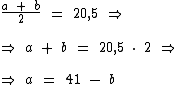
Agora para que possamos solucionar a segunda equação, é necessário que fiquemos com apenas uma variável na mesma. Para conseguirmos isto iremos substituir a por 41 - b:
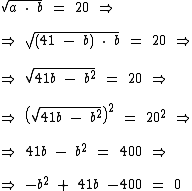
Note que acabamos obtendo uma equação do segundo grau:
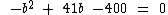
Solucionando a mesma temos:
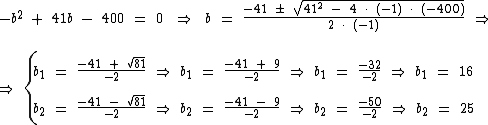
O número b pode assumir, portanto os valores 16 e 25.
É de se esperar, portanto que quando b for igual a 16, que a seja igual a 25 e quando b for igual a 25, que a seja igual a 16. Vamos conferir.
Sabemos que 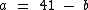 , portanto atribuindo a b um de seus possíveis valores, iremos encontrar o valor de a.
, portanto atribuindo a b um de seus possíveis valores, iremos encontrar o valor de a.
Para b = 16 temos:
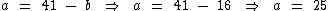
Para b = 25 temos:
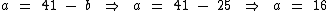
Concluindo:
 Os dois números são 16 e 25.
Os dois números são 16 e 25.
 7) A média geométrica entre dois números é igual a 6. Se a eles juntarmos o número 48, qual será a média geométrica entre estes três números?
7) A média geométrica entre dois números é igual a 6. Se a eles juntarmos o número 48, qual será a média geométrica entre estes três números?
Se chamarmos de P o produto destes dois números, a partir do que foi dito no enunciado podemos montar a seguinte equação:
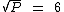
Elevando ambos os membros desta equação ao quadrado, iremos obter o valor numérico do produto destes dois números:
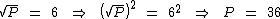
Agora que sabemos que o produto de um número pelo outro é igual 36, resta-nos multiplicá-lo por 48 e extraímos a raiz cúbica deste novo produto para encontrarmos a média desejada:
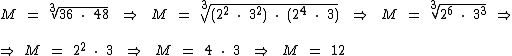
Note que para facilitar a extração da raiz cúbica, realizamos a decomposição dos números 36 e 48 em fatores primos. Acesse a página decomposição de um número natural em fatores primos para maiores informações sobre este assunto.
Respondendo à pergunta:
 Ao juntarmos o número 48 aos dois números iniciais, a média geométrica passará a ser 12.
Ao juntarmos o número 48 aos dois números iniciais, a média geométrica passará a ser 12.
 8) Um comerciante pretende misturar 30 kg de um produto A, que custa R$ 6,80/kg com um produto B que custa R$ 4,00/kg para obter um produto de qualidade intermediária que custe R$ 6,00/kg. Quantos quilogramas do produto B serão utilizados nesta mistura?
8) Um comerciante pretende misturar 30 kg de um produto A, que custa R$ 6,80/kg com um produto B que custa R$ 4,00/kg para obter um produto de qualidade intermediária que custe R$ 6,00/kg. Quantos quilogramas do produto B serão utilizados nesta mistura?
Interpretando o enunciado, entendemos que devemos somar o valor total de dois produtos e depois dividir este total pela soma da quantidade destes dois produtos, de sorte que o resultado, ou seja, a média, resulte em R$ 6,00/kg.
A representação matemática desta situação pode ser vista abaixo:
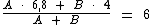
Como sabemos que A = 30, vamos substituí-lo na equação a fim de podermos encontrar o valor de B:
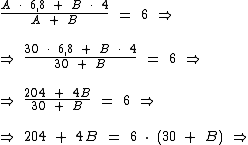
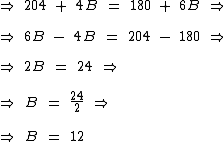
Portanto:
 12 kg do produto B serão utilizados nesta mistura para que o quilograma do produto final custe R$ 6,00.
12 kg do produto B serão utilizados nesta mistura para que o quilograma do produto final custe R$ 6,00.
 9) A média das notas dos 50 alunos de uma classe e 7,7. Se considerarmos apenas as notas dos 15 meninos, a nota média é igual a 7. Qual a média das notas se considerarmos apenas as meninas?
9) A média das notas dos 50 alunos de uma classe e 7,7. Se considerarmos apenas as notas dos 15 meninos, a nota média é igual a 7. Qual a média das notas se considerarmos apenas as meninas?
Nesta classe de 50 alunos temos 15 meninos e consequentemente temos 35 meninas.
Se somarmos a pontuação total obtida pelas meninas, à pontuação total obtida pelos meninos e dividirmos o valor desta soma pelo número de alunos da classe, iremos obter a sua média que é igual a 7,7.
Como sabemos, ao multiplicarmos o valor da média pela quantidade de elementos, obtemos o somatório dos mesmos.
Em função do explanado acima, para solucionar o problema vamos montar uma equação onde chamaremos de x a média das notas das meninas:
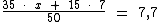
Solucionando a equação temos:
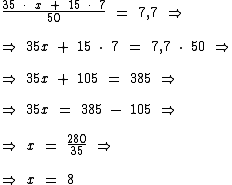
Logo:
 A média das notas das meninas é igual a 8.
A média das notas das meninas é igual a 8.
 10) A média aritmética simples de 4 números pares distintos, pertencentes ao conjunto do números inteiros não nulos é igual a 44. Qual é o maior valor que um desses números pode ter?
10) A média aritmética simples de 4 números pares distintos, pertencentes ao conjunto do números inteiros não nulos é igual a 44. Qual é o maior valor que um desses números pode ter?
Quando falamos de média aritmética simples, ao diminuirmos um dos valores que a compõe, precisamos aumentar a mesma quantidade em outro valor, ou distribuí-la entre vários outros valores, de sorte que a soma total não se altere, se quisermos obter a mesma média.
Neste exercício, três dos elementos devem ter o menor valor possível, de sorte que o quarto elemento tenha o maior valor dentre eles, tal que a média aritmética seja igual a 44. Este será o maior valor que o quarto elemento poderá assumir.
Em função do enunciado, os três menores valores inteiros, pares, distintos e não nulos são: 2, 4 e 6.
Identificando como x este quarto valor, vamos montar a seguinte equação:
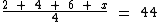
Solucionando-a temos:
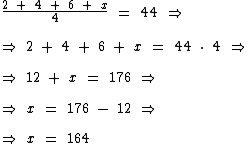
Assim sendo:
 O maior valor que um desses números pode ter é 164.
O maior valor que um desses números pode ter é 164.





