Exercícios resolvidos - Progressão Aritmética

Sabemos que todos os números naturais são múltiplos de si mesmos exceto o zero, então neste exercício tratamos de uma P.A. que se inicia no número 15 e de quinze em quinze termina no número 90, que é o maior número com dois dígitos que é divisível por 15, ou seja, que é o maior múltiplo de quinze com dois dígitos.

Então os dados que possuímos para a resolução do problema são:

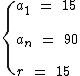
Através da fórmula do termo geral vamos identificar o número de termos desta P.A.:

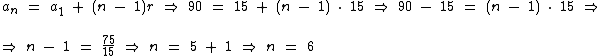
Portanto a referida P.A. possui 6 termos.

Apenas para que você possa conferir, veja abaixo a P.A. completa:

P.A. ( 15, 30, 45, 60, 75, 90 )

Logo:

O número 15 possui 6 múltiplos com 2 dígitos.

Sabemos que com exceção dele próprio, o número zero é múltiplo de todos os números naturais, então estamos tratando da seguinte P.A.:

P.A. ( 0, 21, 42, ..., a₃₀ )

Estamos em busca do termo a₃₀, sendo que dispomos dos seguintes dados:

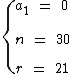
Através da fórmula do termo geral vamos identificá-lo:

Logo:

O trigésimo múltiplo do número natural 21 é 609.

Como esta sucessão possui 39 termos, sabemos que o termo central é o a₂₀, que possui 19 termos à sua esquerda e mais 19 à sua direita. Então temos os seguintes dados para solucionar a questão:

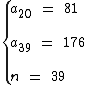
Sabemos também que a soma de dois termos equidistantes dos extremos de uma P.A. finita é igual à soma dos seus extremos. Como esta P.A. tem um número ímpar de termos, então o termo central tem exatamente o valor de metade da soma dos extremos.

Em notação matemática temos:

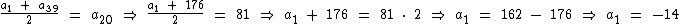
Assim sendo:

O primeiro termo desta sucessão é igual a -14.

Vamos utilizar a fórmula abaixo na resolução do problema:

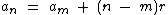
Temos os seguintes dados:

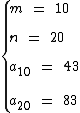
Substituindo-os na fórmula temos:

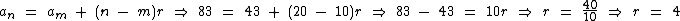
Agora que conhecemos a razão da sucessão, podemos partir do termo a₂₀, poderia ser o termo a₁₀ se assim quiséssemos, para encontrarmos o termo a₃₀:

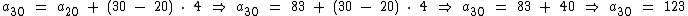
Assim sendo:

O trigésimo termo desta sucessão é igual a 123.

Do enunciado tiramos que o último termo, a₁₀, é igual a 10. Então podemos utilizar a fórmula a seguir para solucionarmos a questão:

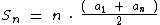
Dispomos dos seguintes dados:

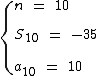
Substituindo-os na fórmula em busca de a₁ temos:

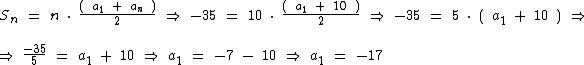
Portanto:

O primeiro termo desta progressão é igual a -17.

Temos os seguintes dados:

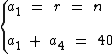
Utilizaremos a fórmula abaixo para representarmos a₄ em função de a₁:

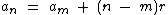
Para n = 4 do termo a₄ e m = 1 do termo a₁, temos:

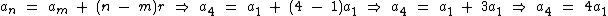
Portanto a₄ = 4a₁ e como sabemos que a₁ + a₄ = 40 temos:

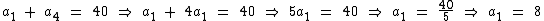
Como temos uma P.A. com 8 termos, que se inicia em 8 e cuja razão também é igual a 8 temos:

A P.A. procurada é P.A. ( 8, 16, 24, 32, 40, 48, 56, 64 ).

Na resolução deste problema utilizaremos a seguinte fórmula:

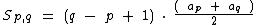
Temos os seguintes dados:

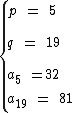
Substituindo estes dados na fórmula acima temos:

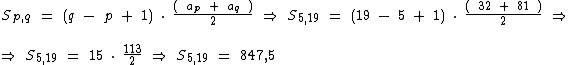
Portanto:

A soma do quinto ao décimo-nono termo desta P.A. é igual a 847,5.

Temos então a seguinte progressão aritmética:

P.A. ( a₁, a₂, a₃ )

Como visto na parte teórica, sabemos que podemos representar um termo em função de outro, através da adição ou da subtração da razão, de n vezes a razão, onde n é a quantidade de termos deslocados de um ao outro.

Pensando nisto podemos eleger o termo a₂ para representarmos todos os outros em função dele, assim:

P.A. ( a₂ - r, a₂, a₂ + r )

Mas por que foi escolhido o termo a₂ e não o a₁, por exemplo?

Caso tivéssemos escolhido o termo a₁ teríamos:

P.A. ( a₁, a₁ + r, a₁ + 2r )

Repare que como a₂ é o termo central, ao escolhê-lo temos a possibilidade de eliminarmos a razão r e encontramos o seu valor ao somarmos todos os termos da P.A., vejamos:

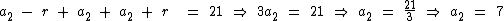
No entanto podemos ver que se tivéssemos escolhido o termo a₁ isto não seria possível:

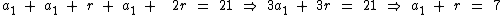
Note que neste caso teríamos uma expressão com duas variáveis, o que não nos permitiria obter o valor das mesmas a partir de uma única sentença.

Agindo de forma análoga, na expressão do produto iremos escrever os demais termos também em função de a₂, visto que este é um valor já identificado:

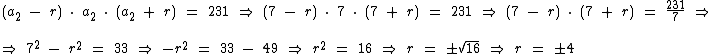
Visto que a P.A. é decrescente, a sua razão é negativa. Como a₂ = 7, r = -4 e a₃ = a₂ + r, temos que:

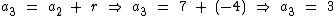
Logo:

O valor do último termo desta P.A. é igual a 3.

Sabemos que através da fórmula abaixo podemos calcular a soma dos n primeiro termos de uma progressão aritmética. Com o auxílio dela iremos solucionar o problema.

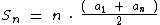
Para a soma dos 5 primeiros termos temos:

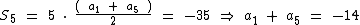
Para a soma dos 10 primeiros termos temos:

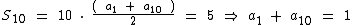
Expressando estas duas equações em função de a₁ temos:

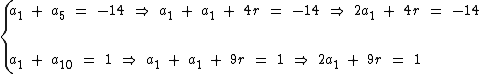
Multiplicando 2a₁ + 4r = -14 por -1 e somando com 2a₁ + 9r = 1, temos:

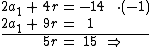
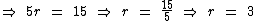
Tendo conhecimento do valor da razão, podemos identificar o valor de a₁ na expressão 2a₁ + 9r = 1:

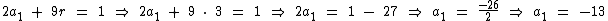
Finalmente conhecendo-se o valor de a₁ e da razão, podemos calcular a soma dos 15 primeiros termos:

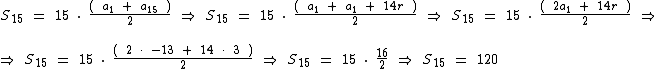
Assim sendo:

A soma dos 15 primeiros termos desta P.A. é igual a 120.

Primeiramente iremos calcular a razão da progressão aritmética:

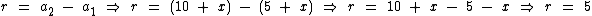
Agora temos como calcular o seu número de termos:

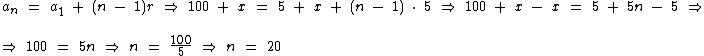
Finalmente iremos calcular o valor de x:

Portanto:

O valor de x é 3.