 O saldo de contratações no mercado formal no setor varejista da região metropolitana de São Paulo registrou alta. Comparando as contratações deste setor no mês de fevereiro com as de janeiro deste ano, houve incremento de 4 300 vagas no setor, totalizando 880 605 trabalhadores com carteira assinada.
O saldo de contratações no mercado formal no setor varejista da região metropolitana de São Paulo registrou alta. Comparando as contratações deste setor no mês de fevereiro com as de janeiro deste ano, houve incremento de 4 300 vagas no setor, totalizando 880 605 trabalhadores com carteira assinada.
Disponível em: http://www.folha.uol.com.br. Acesso em: 26 abr. 2010 (adaptado).
Suponha que o incremento de trabalhadores no setor varejista seja sempre o mesmo nos seis primeiros meses do ano.
Considerando-se que y e x representam, respectivamente, as quantidades de trabalhadores no setor varejista e os meses, janeiro sendo o primeiro, fevereiro, o segundo, e assim por diante, a expressão algébrica que relaciona essas quantidades nesses meses é
- A) y = 4 300x
- B) y = 884 905x
- C) y = 872 005 + 4 300x
- D) y = 876 305 + 4 300x
- E) y = 880 605 + 4 300x
Este problema descreve uma situação que matematicamente podemos representar através de uma função polinomial do 1° grau.
As funções afins, como também são denominadas, definidas de 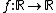 possuem a forma:
possuem a forma: 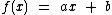 , com
, com 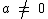 (
(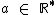 e
e 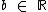 )
)
O coeficiente a é o coeficiente angular da reta do gráfico da função. Através deste coeficiente podemos determinar se uma função afim é crescente ou decrescente.
Neste problema temos a = 4300, que é o crescimento mensal do número de vagas no setor.
Fazendo y = f(x) temos:
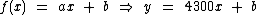
Segundo o enunciado, em fevereiro (x = 2) o número de trabalhadores com carteira assinada (y) era de 880605:
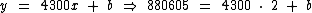
Agora temos condições de calcular o valor do coeficiente b, o que nos permitirá definir a expressão procurada:
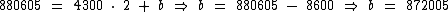
Substituindo o valor de b por 872005 chegamos a esta expressão:
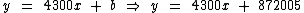
Vamos inverter os termos do segundo membro, apenas para efeito de comparação visual com as alternativas disponíveis:
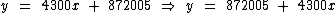
 C é a alternativa correta.
C é a alternativa correta.




