Resolução Passo a Passo de Questões de Concursos Públicos - II
1) Usando os conceitos, índices e multiplicadores, podemos dizer que a inflação acumulada, aproximada a centésimos, de um trimestre, cujas inflações mensais foram de 1,5%, 1,4% e 0,8%, foi de quantos por cento?
A resolução desta questão se resume a encontrar um único fator percentual que substitua os três percentuais apresentados. Para fazê-lo iremos obter os fatores referentes a cada um dos três percentuais e multiplicá-los.
Para acrescentarmos 1,5% a um valor, devemos multiplicá-lo por 1,015:
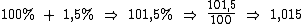
O 100% que indica que estamos fazendo um acréscimo ao valor original, neste caso um acréscimo de 1,5%. Então o fator referente a 1,5% de acréscimo é 1,015.
Se não estivéssemos fazendo um acréscimo, mas apenas calculando 1,5%, o fator seria apenas 0,015:
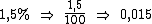
Voltando ao problema, de forma análoga o fator referente a 1,4% de acréscimo é:
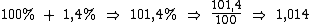
Para o terceiro percentual de 0,8% de acréscimo o fator é:
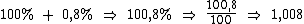
Agora para obtermos o fator de acréscimo equivalente devemos multiplicá-los:
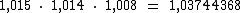
Na forma percentual será:
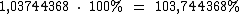
Como o enunciado pede uma precisão de centésimos, devemos utilizar apenas duas casas decimais:
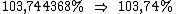
O problema ainda não está concluído.
Este percentual nos indica que um produto que fosse reajustado por estes percentuais de inflação, iria estar custando agora 103,74% do valor original, como o percentual de 100% se refere ao seu valor original, a inflação acumulada será de 3,74%:
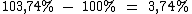
Portanto:
A inflação acumulada do trimestre aproximada a centésimos é de 3,74%.
2) Um motorista faz um percurso em três etapas. A primeira etapa faz em 1/5 do tempo total T utilizado. Na segunda etapa, ele leva 1/4 do tempo. Se o restante do tempo foi utilizado na etapa final, esse tempo em relação ao tempo T utilizado, vale quanto em porcentagem?
Nesta questão vamos transformar as frações em números decimais e somando-os veremos quanto falta para 1, que nesta questão equivale a 100% do tempo utilizado.
Poderíamos trabalhar com frações e no final transformá-las em porcentagem, mas como estas frações não são geratrizes de dízimas periódicas, é mais conveniente trabalharmos com números decimais.
1/5 é igual a 1 dividido por 5:
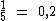
E 1/4 é igual a 1 dividido por 4:
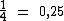
0,2 mais 0,25 para 1 faltam 0,55:
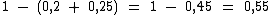
Este é o valor procurado, mas em decimal. Na forma percentual temos:
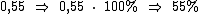
Então:
O tempo utilizado na etapa final vale 55% do tempo total T.
3) Uma lanchonete disponibiliza aos seus clientes 6 tipos de lanches quentes, 3 tipos de lanches frios, 7 tipos de sucos naturais e 4 tipos de sobremesas, todos de tipos diferentes. Se um jovem quiser pedir um lanche quente, um lanche frio, um copo de suco e uma sobremesa, então a quantidade de opções diferentes com que ele poderia fazer o seu pedido seria qual?
Na resolução deste problema vamos recorrer à análise combinatória, mais precisamente ao princípio fundamental da contagem.
Segundo o princípio fundamental da contagem, um evento que ocorre em 4 situações independentes e sucessivas, tendo a primeira situação ocorrendo de 6 maneiras, a segunda ocorrendo de 3 maneiras, a terceira situação ocorrendo 7 e a quarta 4, temos que o número total de ocorrências será dado pelo produto:
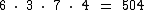
Isto é fácil de intuirmos se pensarmos da seguinte forma:
Como temos 6 tipos de lanches quentes, para cada um dos 3 tipos de lanches frios teríamos 6 opções de escolha de lanches quentes. Vejamos:
Q1F1, Q2F1, Q3F1, Q4F1, Q5F1, Q6F1;
Q1F2, Q2F2, Q3F2, Q4F2, Q5F2, Q6F2;
Q1F3, Q2F3, Q3F3, Q4F3, Q5F3, Q6F3.
Perceba que temos 6 . 3 combinações distintas, ou seja, 18 combinações.
Como temos 18 combinações de lanches quentes com lanches frios, para cada um dos 7 tipos de sucos naturais teríamos 18 opções de escolha de lanche quente/frio, isto é, 18 . 7 combinações distintas, ou seja, 126 combinações distintas.
Para os 4 tipos de sobremesas disponíveis, seguindo este mesmo raciocínio teríamos 126 . 4 combinações distintas, portanto, 504 combinações.
Logo:
A quantidade de opções diferentes com que o jovem poderia fazer o seu pedido seria igual a 504.
4) Joel foi contratado para vender um de notebook, cujo preço unitário é de R$ 1.800,00. Por mês, ele recebe uma quantidade fixa de R$ 600,00. Para além desse valor, recebe ainda uma comissão de 10% do preço de cada notebook vendido. Para receber, num mês, exatamente R$ 4.200,00, qual é o número de notebooks que ele deverá vender?
Precisamos saber qual é o valor a receber em comissões, descontando-se o valor fixo de R$ 600,00, depois sabendo quantos reais são recebidos de comissão em cada venda, vamos calcular o número necessário de vendas para que Joel possa atingir a sua meta.
Para que Joel receba R$ 4.200,00 no total, descontado o salário fixo, ele precisa obter R$ 3.600,00 em comissões:
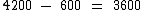
Em cada venda ele acumula R$ 180,00 em comissão:
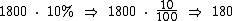
Logo para acumular R$ 3.600,00 em comissões, com parcelas de R$ 180,00 por venda, ele precisará realizar 20 transações para atingir a sua meta:
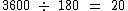
Portanto:
Joel deverá vender 20 de notebooks.
5) Antônio e seu amigo João, sem saberem da coincidência, compraram no mesmo dia televisores de LCD para assistirem aos jogos da Copa 2010. O Antônio gostou de um modelo que custava R$ 1.200,00 e comprou-o com um desconto de 15%. O João comprou outro modelo, que só tinha 5% de desconto. Mais tarde, eles descobriram que, apesar das percentagens de desconto terem sido diferentes, o valor dos dois descontos, em reais, foi igual. Quanto custava na loja o modelo de televisor LCD que João comprou sem o desconto?
Simples assim, primeiro vamos calcular 15% de R$ 1.200,00, depois fazendo o cálculo inverso, vamos descobrir de qual valor o resultado obtido é 5%, já que os descontos, em reais, foram iguais.
15% de R$ 1.200,00 é igual a R$ 180,00:
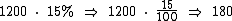
Finalmente R$ 180,00 é igual a 5% de R$ 3.600,00:
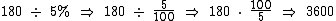
Então:
Sem o desconto, o modelo de televisor LCD que João comprou custava R$ 3.600,00.
6) Trafegando por uma via, um motorista chegou a uma rotatória que dá acesso a outras três vias, sendo uma delas aquela que o levará ao destino esperado. Considerando que não há ali sinalização, qual é a probabilidade de o motorista escolher a via correta?
Nesta questão a probabilidade procurada é a razão do número de vias corretas, para o número total de vias.
Podemos representar o nosso espaço amostral da seguinte forma:
S = { Via Correta, Via Errada 1, Via Errada 2 }
Como o que nos interessa é o caminho correto, o evento E, de o motorista encontrar este caminho, pode ser assim representado:
E = { Via Correta }
Então o número de elementos de E é n(E) = 1 e o número de elementos de S é n(S) = 3, portanto temos a seguinte probabilidade de o motorista seguir o caminho correto:
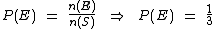
O resultado também pode ser expresso na forma de porcentagem:
Então:
A probabilidade de o motorista escolher a via correta é 1/3 ou aproximadamente 33,33%.
7) Um trabalhador, para poder se aposentar, deve fazer a seguinte conta: somar sua idade com seu tempo de contribuição. Se essa soma der 95, ele pode solicitar aposentadoria. Supondo que Paulo começou a trabalhar e a contribuir para a previdência com 27 anos e nunca mais parou, ele poderá solicitar sua aposentadoria quando estiver, no mínimo, com quantos anos?
Como a cada ano que passa, aumenta em um ano tanto a idade do trabalhador, quanto o seu tempo de contribuição, precisamos calcular quantos anos equivalem à metade da diferença entre 27 e 95, pois a cada ano contamos na verdade dois anos, um da idade e outro da contribuição. Descoberto este valor devemos somá-lo aos 27 anos da idade inicial.
Algebricamente podemos resolver a questão atribuindo a letra n à variável que representa o número de anos decorridos e montando a equação abaixo:
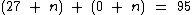
Perceba que ela reflete a parte inicial do que foi dito no primeiro parágrafo. O termo (27 + n) representa a idade do trabalhador no decorrer dos anos (a partir dos 27 anos), já o termo (0 + n) representa o seu tempo de contribuição (O 0 indica que ele nunca havia contribuído até então).
Vamos calcular o valor de n:
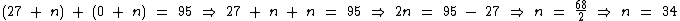
É preciso que se passem 34 anos e como o trabalhador começou a contribuir com 27 anos, ele poderá se aposentar ao chegar aos 61 anos de idade:
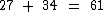
Portanto:
O trabalhador poderá solicitar a sua aposentadoria quando estiver no mínimo com 61 anos de idade.
8) Um elevador pode levar 25 adultos ou 30 crianças. Se 20 adultos já estão no elevador, quantas crianças podem ainda entrar nesse elevador?
A resolução desta questão se baseia na razão do número de crianças que o elevador pode transportar, para o número de adultos da sua capacidade de transporte.
A referida razão é:
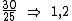
Esta razão nos informa que no lugar de 1 adulto podemos transportar 1,2 crianças.
Como no elevador já estão 20 adultos e cabem no máximo 25, os 5 adultos que faltam para completar a lotação do elevador podem ser substituídos por 6 crianças:
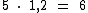
O problema já está resolvido, mas vale aqui dar um alerta.
Digamos que utilizando a mesma razão de 1,2 crianças para 1 adulto, se já estivessem 6 crianças no elevador e se quisesse saber quantos adultos ainda poderiam entrar, qual seria a conta já que ainda restaria espaço para 24 crianças? Veja:
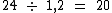
Note que agora ao invés de realizarmos uma multiplicação como no caso anterior, realizamos uma divisão. Quando devemos realizar uma operação e quando devemos realizar a outra?
A nossa razão é 1,2 crianças : 1 adulto. A grandeza do antecedente é criança e a grandeza do consequente é adulto.
No problema original a grandeza que procurávamos, criança, é a mesma grandeza do antecedente da razão, neste caso multiplicamos.
Na segunda hipótese a grandeza procurada é adulto, a mesma grandeza do consequente da razão, neste caso então devemos dividir.
Portanto fique atento.
Ainda podem entrar 6 crianças no elevador.
9) Uma calçada tem a forma de um triângulo retângulo de perímetro igual a 60 m, cujos lados estão em Progressão Aritmética de razão 5. Qual é a área dessa calçada?
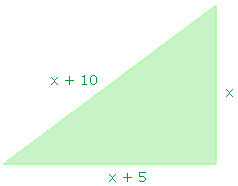
Neste problema precisamos saber calcular o perímetro e a área de um triângulo retângulo, assim como ter um conhecimento mínimo sobre progressões aritméticas.
Segundo o enunciado, podemos concluir que o nosso triângulo é semelhante ao triângulo da figura ao lado.
Já que seus lados estão em progressão aritmética de razão 5, atribuímos ao menor dos catetos o comprimento x. Ao outro cateto atribuímos o valor x + 5 e a hipotenusa atribuímos o valor x + 10, sempre respeitando a razão da P.A.
Como o perímetro de qualquer polígono é igual à soma dos comprimentos dos seus lados, podemos montar a seguinte equação:
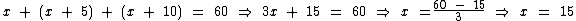
Então a base deste triângulo mede 20 m e sua altura é igual a 15 m.
Como a área de um triângulo é igual ao produto da medida da base pela altura dividido por dois, a área deste triângulo é dada por:
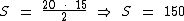
Logo:
A área dessa calçada mede 150 m2.
10) O quinto termo de uma progressão aritmética é 44. Sendo a razão desta progressão igual a 6, qual é a soma entre o primeiro e o centésimo termo dessa progressão?
Nesta questão trabalhamos apenas com progressões aritméticas. Precisamos conhecer ao menos conhecer a fórmula do termo geral de uma P.A.
Esta é a fórmula que temos abaixo:
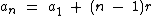
Sabendo que a razão é igual a 6 e que o quinto termo é igual a 44 podemos facilmente calcularmos o valor do primeiro termo:
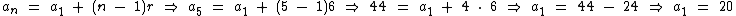
Já que a1 é igual a 20, a100 será:
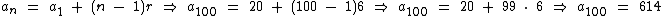
Logo a soma do primeiro e do último termo é:
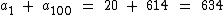
Portanto:
A soma entre o primeiro e o centésimo termo dessa progressão é igual a 634.
