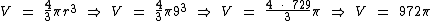Sólidos Geométricos - Área e Volume da Esfera
A Esfera é um sólido geométrico com uma superfície fechada cuja distância entre o seu ponto central é a mesma para qualquer ponto da sua superfície.
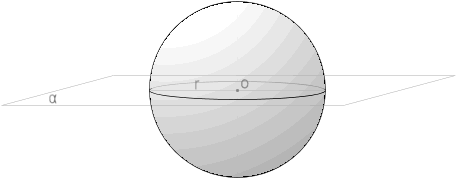
Um plano α que contenha o ponto O, centro da esfera, irá dividi-la em duas semiesferas.
Veja na figura que um círculo cujo centro seja também o centro da esfera e cujos pontos da sua circunferência também sejam pontos da superfície desta esfera, a dividirá em duas partes iguais, exatamente duas semiesferas.
Observe que o raio r deste círculo é também o raio desta esfera.
Cálculo da Área da Superfície da Esfera
A área total da superfície de uma esfera é igual ao quádruplo do produto de  pelo quadrado do raio da esfera:
pelo quadrado do raio da esfera:
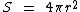
Exemplo de Cálculo da Área da Superfície da Esfera
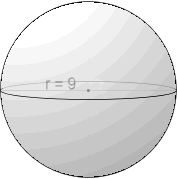
Na figura ao lado temos uma esfera cuja medida do seu raio é igual a 9. Vamos calcular a área total da sua superfície através da fórmula vista acima:
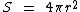
A figura nos fornece o raio da esfera:
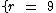
Substituindo tais informações na fórmula obtemos a área total da esfera:
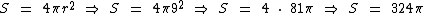
Cálculo do Volume da Esfera
Se conhecemos a medida do raio de uma esfera, o seu volume pode ser calculado através da seguinte fórmula:
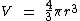
Exemplo de Cálculo do Volume da Esfera

Vamos calcular o volume da mesma esfera vista no exemplo anterior.
Como visto acima, a figura nos fornece a medida do raio da esfera:
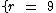
Calcularemos o volume da esfera através da fórmula:
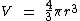
Substituindo a variável r por seu valor numérico 9: