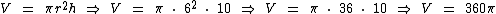Sólidos Geométricos - Área e Volume do Cilindro
O Cilindro é um sólido geométrico delimitado por duas bases circulares congruentes, contidas em diferentes planos paralelos e por uma superfície lateral formada por todas as suas geratrizes.
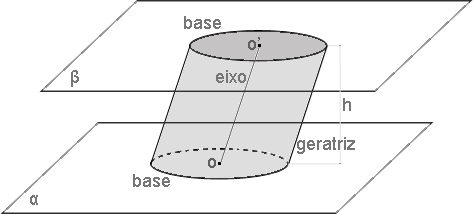
Uma geratriz de um cilindro circular é qualquer segmento de reta paralelo ao eixo do cilindro e com extremidades nas circunferências das bases.
O eixo de um cilindro circular é o segmento de reta cujos extremos são os centros das bases do cilindro.
A altura de um cilindro circular é a distância entre os círculos (planos) das bases.
Cilindro Circular Reto ou Oblíquo
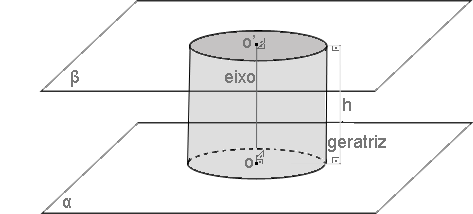
Um cilindro circular reto possui o seu eixo e as suas geratrizes perpendiculares aos planos das bases e o eixo e as geratrizes são congruentes à sua altura.
A projeção ortogonal do centro de uma das bases no plano da outra é o centro da outra base, ou seja, visto o cilindro de cima os centros se sobrepõe, na verdade as bases se sobrepõem.
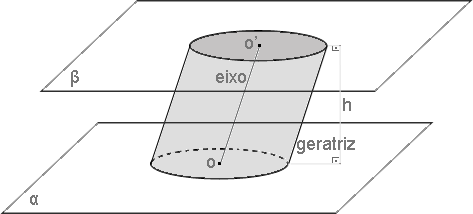
Um cilindro circular oblíquo possui o seu eixo e as suas geratrizes oblíquas aos planos das bases e o eixo e as geratrizes não são congruentes à sua altura.
A projeção ortogonal do centro de uma das bases no plano da outra não é o centro da outra base, isto é, observado o cilindro de cima os centros das bases não se sobrepõem
Cálculo da Área da Superfície do Cilindro Circular
A área total da superfície de um cilindro circular é a soma da área da superfície lateral com a área dos dois círculos das bases.
A área da superfície lateral é igual ao produto do perímetro da base pela altura do cilindro:
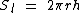
A área de cada base é igual ao produto de 
pelo quadrado do raio da base, visto que as base são círculos:
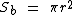
Para não precisarmos calcular as áreas separadamente, podemos utilizar uma única fórmula:
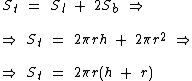
h se refere a altura do cilindro e r ao raio das suas bases. Sl, Sb e St se referem respectivamente a área lateral, a área das bases e a área total.
Exemplo de Cálculo da Área da Superfície do Cilindro Circular
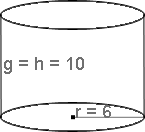
A partir dos dados obtidos da figura geométrica ao lado vamos calcular a área total da sua superfície.
Temos a figura de um cilindro circular reto. Como podemos observar, as geratrizes e a altura possuem a mesma medida.
Vamos calcular a área do cilindro circular através da fórmula vista acima:
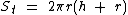
A figura nos fornece os seguintes dados:
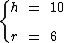
Substituindo tais informações na fórmula obtemos a área total do cilindro:
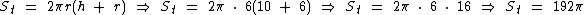
Cálculo do Volume do Cilindro Circular
Independentemente de um cilindro circular ser reto ou oblíquo, a medida do seu volume é igual ao produto da área da base pela altura do cilindro, o qual podemos expressar através da seguinte fórmula:
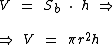
Exemplo de Cálculo do Volume do Cilindro Circular
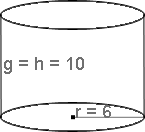
Vamos calcular o volume do cilindro reto visto no exemplo anterior.
Os dados fornecidos pela figura são:
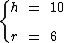
Realizaremos o cálculo do volume do cilindro circular através desta fórmula:
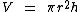
Substituindo as variáveis pelos valores:
