Exercícios resolvidos - Sólidos Geométricos - Cálculo de Área e Volume

Na parte teórica vimos que a área da superfície de uma esfera pode ser calculada através da seguinte fórmula:

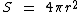
Vimos também que o volume de uma esfera pode ser calculado por esta outra fórmula:

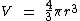
Como podemos observar, para realizarmos o cálculo do volume da esfera precisamos conhecer a medida do seu raio. Tal medida pode ser obtida através da fórmula do cálculo da área, visto que a área é informada no enunciado do exercício:

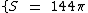
Substituindo a medida da área na respectiva fórmula de cálculo temos:

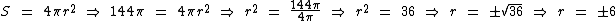
Como a medida do raio não pode ser um valor negativo, desprezamos o valor -6 e consideramos apenas o valor 6.

Agora podemos calcular o volume da esfera utilizando a fórmula apropriada:

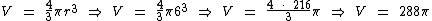
O volume desta esfera é 288π cm³.

Para calcularmos o volume da caixa ainda precisamos conhecer a sua altura, visto que o seu comprimento e a sua largura já são fornecidos pelo enunciado do exercício, assim como a sua área que será utilizada na sequência:

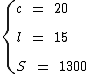
Como dispomos do comprimento e da largura das bases do prisma, então podemos calcular a área de cada uma delas:

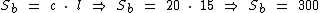
A área total de um prisma é igual a soma do valor da área das duas bases mais a área de todas as suas faces laterais:

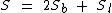
Como já conhecemos a área total (1300) e a área de cada uma das bases (300), podemos calcular a área das superfícies laterais:

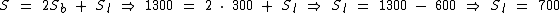
Como sabemos, podemos calcular a soma das áreas de todas as faces laterais de um paralelepípedo multiplicando-se o perímetro de uma das faces base pela medida da altura do paralelepípedo:

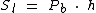
O perímetro da base nada mais é que a soma das medidas de todos os seus lados, que podemos representar através da seguinte fórmula:

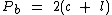
Ao substituirmos P_b na fórmula anterior chegamos a:

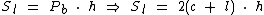
Substituindo as variáveis com valores conhecidos descobrimos a altura do prisma:

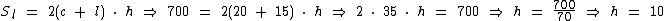
Finalmente podemos calcular o volume da caixa:

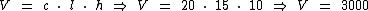
O volume desta caixa deve ser de 3000 cm³.

O enunciado nos fornece a área lateral e o volume do cilindro:

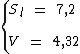
Utilizamos a fórmula abaixo para o cálculo da área lateral de um cilindro:

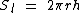
Já o cálculo do seu volume pode ser realizado através desta outra fórmula:

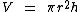
Note o que iremos obter ao multiplicarmos a fórmula da superfície lateral por r e a dividirmos por 2:

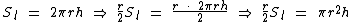
Percebeu que no segundo membro obtivemos o segundo membro da fórmula de cálculo do volume do cilindro?

Então podemos expressar a área em função do volume:

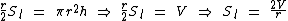
Ou vice-versa, expressando o volume em função da área:

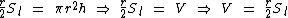
Como conhecemos o valor numérico de V e de S_l, estamos a dois passos de solucionarmos o problema, ao utilizarmos a expressão da superfície lateral em função do volume para calcularmos a medida do raio da base do cilindro:

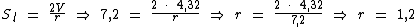
Ou, ao utilizarmos a expressão do volume em função da superfície lateral, na obtenção da medida do raio da base do cilindro:

E finalmente calculando a sua altura, seja pela substituição da medida do raio na fórmula do volume:

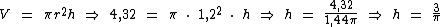
Ou na fórmula da superfície lateral:

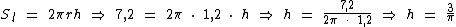
A medida da altura deste recipiente é de ³/_π m.

Sendo r a medida do raio da base deste cone e h a medida da sua altura, do enunciado temos as seguintes informações:

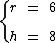
Como r e h são conhecidos, podemos calcular o volume do cone circular reto através da seguinte fórmula:

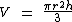
Então vamos substituir o valor numérico destas variáveis na fórmula e executar as operações por ela apontadas:

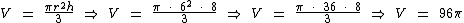
Portanto, o volume do cone circular reto é igual a 96π cm³.

Temos ainda que calcular a área da superfície do cone circular reto, que pode ser obtida através desta outra fórmula:

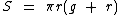
Nesta fórmula a variável g representa a medida da geratriz do cone. Caso você tenha dúvida sobre o conceito de geratriz de um cone circular, acesse o artigo Sólidos Geométricos - Área e Volume do Cone Circular onde, dentre outros, também apresentamos este conceito.

Note que não possuímos o valor da geratriz, no entanto no referido artigo vimos que se conhecemos a altura do cone circular reto e também o raio da sua base, podemos obtê-la recorrendo ao Teorema de Pitágoras:

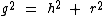
Substituindo os valores conhecidos temos:

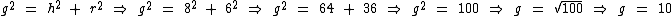
Agora já podemos calcular a área da superfície do cone:

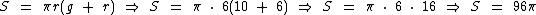
Então, 96π cm² é a medida a área da superfície do cone.

O volume do cone é igual a 96π cm³ e a área da sua superfície é igual a 96π cm².

De acordo com o enunciado, trata-se de uma pirâmide na qual o polígono da base é um quadrado cuja medida de seus lados é igual a altura da pirâmide.

É sabido que a área do quadrado é igual ao quadrado da medida de seus lados. Como sabemos que a sua área é igual a 9 cm², podemos calcular a medida dos seus lados:

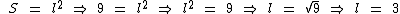
Como visto na parte teórica, a medida do volume de uma pirâmide é igual a um terço do produto da área da sua base pela sua altura.

Do enunciado, a área da sua base é igual a 9 cm² e sua altura, calculada acima, é igual a 3 cm.

O volume da pirâmide pode ser calculado através da seguinte fórmula:

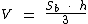
Substituindo nesta fórmula os valores conhecidos:

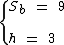
Calculando temos:

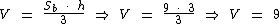
O volume da pirâmide é igual a 9 cm³.