Exercícios resolvidos - Cálculo da Área de Figuras Planas
Para maiores informações teóricas sobre este assunto veja também:Cálculo da Área de Figuras Planas
Nos exercícios onde for necessário, use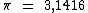 
1) Uma professora deu aos seus alunos uma folha de papel retangular com 1m de largura e 80cm de altura, para que seja recortada em quadrados iguais, de sorte que não haja sobra de papel e que os quadrados tenham o maior tamanho possível. Qual será a área de cada uma destes quadrados?
Como a professora deseja que sejam formados vários quadrados iguais a partir da folha de 100cm x 80cm, percebemos que a medida dos lados destes quadrados deve ser divisora tanto de 100, quanto de 80, para que não haja sobras e como queremos que cada um destes quadrados tenha a maior área possível, então a medida dos lados destes quadrados deve ser o maior divisor comum a 100 e 80, ou seja, precisamos calcular o MDC(100, 8) para encontrarmos a medida dos lados de cada quadrado.
Na página Máximo Divisor Comum - MDC explicamos em detalhes o cálculo do MDC e você também pode recorrer à nossa Calculadora MMC / MDC para ver em detalhes como é realizado tal procedimento com os números que vocês especificar.
Através da utilização desta calculadora você poderá ver passo a passo que o cálculo do MDC(100, 80) resulta em 20.
Agora que temos conhecimento da medida dos lados dos quadrados que devem ser recortados pelos alunos, basta calcularmos a área dos mesmos.
Como sabemos o cálculo da área ou superfície de um quadrado é realizado através da fórmula:
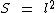
Então multiplicando-se o lado do quadrado por ele mesmo temos:
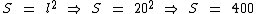
Portanto:
A área de cada uma destes quadrados será de 400cm2.
2) Uma mesa retangular mede 1,2 m x 0,8 m. Se numa das quinas desta mesa eu fixar um barbante com um prego, qual deve ser o tamanho aproximado do barbante de sorte que eu consiga percorrer um setor circular com um terço da área da mesa?
A área da mesa é igual a:
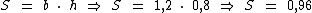
Como temos uma mesa retangular, os ângulos formados nas suas quinas são de 90°. Com estes dados podemos calcular o comprimento que teve ter o barbante para cobrirmos 1/3 da área da mesa, se o utilizarmos como um compasso para traçarmos um setor circular na mesma:
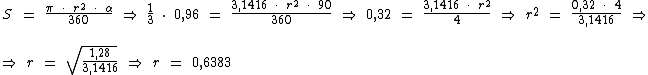
Logo:
O comprimento do barbante deve ser de aproximadamente 0,6383 m.
3) Uma pizza circular tem área de 706,86 cm2. Qual é a área interna da menor caixa quadrada para transportá-la?
Para calcularmos a área interna da caixa precisamos saber a medida interna do seu lado. Esta medida é a mesma medida do diâmetro da pizza, que equivale ao dobro do raio da mesma. Como sabemos a sua área, podemos calcular o seu raio assim:
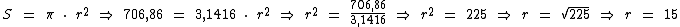
Como o raio da pizza é igual a 15 cm, temos que o seu diâmetro e consequentemente a medida das laterais internas da caixa será o dobro disto, ou seja, 30 cm, logo a área interna da caixa será:
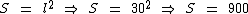
Logo:
A área interna da menor caixa quadrada capaz de transportar esta pizza é de 900 cm2.
4) Se dobrarmos as medidas da base e da altura de um retângulo, em quanto estaremos aumentando a sua área?
Como sabemos a área de um retângulo é calculada segundo a fórmula:
Se dobrarmos as duas medidas teremos:
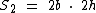
Se dividirmos a fórmula com as medidas dobradas, pela original teremos:
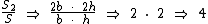
Assim:
Ao dobrarmos as medidas das laterais de um retângulo estaremos quadruplicando a sua área.
5) Um prato tem 24 cm de diâmetro e um outro tem 30 cm. Em termos de área, o prato menor é quantos por cento do maior?
Para calcularmos a área de cada prato, segundo a fórmula devemos multiplicar por 
, o quadrado do seu raio.
Se dividirmos a área do prato menor pela área do prato maior, iremos obter quantos por cento a área do menor é da área do maior, só que na forma decimal. Como o raio é igual à metade do diâmetro temos:
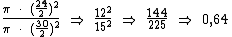
Para encontramos o resultado desejado na forma de porcentagem, basta multiplicarmos 0,64 por 100:
Portanto:
Em termos de área o prato menor é 64% do maior.
