Cálculo da Área de um Polígono Regular
Neste artigo vemos como calcular a área de um polígono regular a partir do seu número de lados e da medida dos mesmos.
Uma linha poligonal fechada é formada por segmentos de reta não alinhados em uma mesma reta e que se fecham.
Polígono é uma figura plana formada por uma linha poligonal fechada.
Polígonos regulares são aqueles que possuem todos os seus lados e ângulos internos congruentes.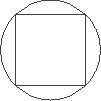
O número de ângulos internos de um polígono é igual ao número de lados do mesmo.
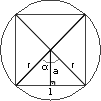
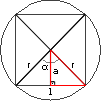
Todo polígono regular pode ser inscrito em uma circunferência, tal qual o quadrado na figura ao lado.
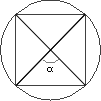
Qualquer polígono regular inscrito em uma circunferência pode ser divido em n triângulos congruentes, onde n é o número de lados do polígono. Neste nosso exemplo n = 4, visto que o polígono regular em questão é um quadrado.
A medida do ângulo α pode ser obtida através da seguinte fórmula:
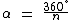
Neste nosso exemplo como n = 4, temos que α = 90°:
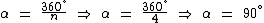
Para obtermos a área deste polígono basta calcularmos a área de um destes triângulos e multiplicá-la por 4, visto que os quatro triângulos são congruentes. No caso de uma figura com n lados iremos multiplicar a área do triângulo por n.
A área de um triângulo é obtida multiplicando-se a medida da sua altura pela medida da sua base e dividindo-se este produto por dois.
A altura do triângulo em questão é um apótema do polígono e a base do triângulo é um lado do polígono.
Denominamos apótema o segmento de reta que interliga perpendicularmente o centro geométrico de um polígono a um dos seus lados. Neste caso o segmento a.
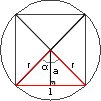
Recorrendo à trigonometria, mais especificamente à lei dos cossenos, vamos escrever uma equação para calcularmos o valor do lado l em função dos lados r e do ângulo α.
A lei dos cossenos nos diz que:
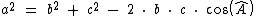
Onde a, b e c são os lados de um triângulo. O ângulo  é o ângulo oposto ao lado a.
Substituindo as variáveis em questão:
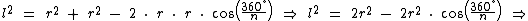
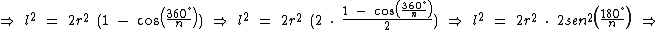
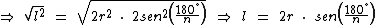
Agora recorrendo ao Teorema de Pitágoras e novamente à trigonometria, vamos escrever o apótema a em função de um lado r e de metade do lado l:

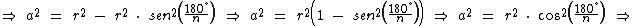
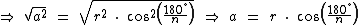
Isolando o raio r nas duas equações temos:
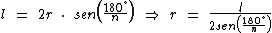
E
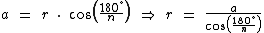
Logo, o apótema a escrito em função do lado l e do ângulo α é igual a:
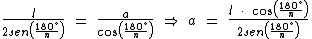
Agora já podemos calcular a área do referido triângulo:
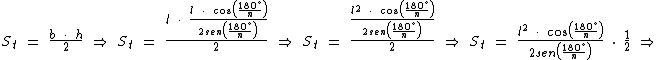
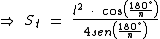
A fórmula acima se refere à área de apenas um dos triângulos, mas como o polígono regular possui n lados devemos multiplicar esta área por n para obtermos a área total do polígono:
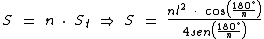
A razão entre o cosseno e o seno de um ângulo pode ser expressa como a cotangente deste ângulo:
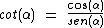
O que nos permite reescrever a fórmula desta forma:
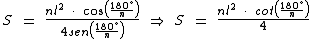
Exemplo de Cálculo da Área do Quadrado
Vamos supor que os lados de um quadrado medem 10 cm cada um.
Os dados do problema são:
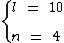
Substituindo tais dados na fórmula temos:
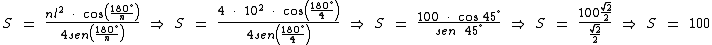
A área do quadrado é igual a 100 cm2 como já era de se esperar, pois como sabemos a área de um quadrado é obtida elevando-se ao quadrado a medida de um dos seus lados:
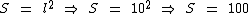
Se tivéssemos utilizado a fórmula da cotangente teríamos chegado ao mesmo resultado:
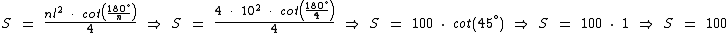
Exemplo de Cálculo da Área do Pentágono Regular
Através da equação mostrada você pode criar uma fórmula para calcular a área de qualquer polígono regular.
Vamos criar uma fórmula para o pentágono regular.
O pentágono é um polígono com cinco lados:
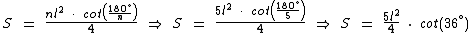
Com o auxílio de uma calculadora ou de uma tabela trigonométrica, vamos calcular através desta fórmula a área de um pentágono regular cujos lados medem 8 cm:
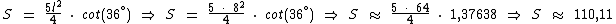
Portanto, a área deste pentágono regular é de aproximadamente 110,11 cm2.
Exemplo de Cálculo da Área do Hexágono Regular
Neste último exemplo vamos criar uma fórmula para o hexágono regular.
O hexágono é um polígono com seis lados:
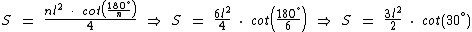
Finalizando este exemplo vamos calcular através desta fórmula a área de um hexágono com lados medindo 6 cm:
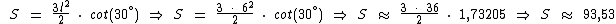
A área deste hexágono regular é de aproximadamente 93,53 cm2.
