Equação do Segundo Grau - Relações entre Coeficientes e Raízes
Através de estudos o matemático Albert Girard definiu relações entre as equações do segundo grau e suas raízes. Estas relações nos permitem obter a equação original a partir de suas raízes, assim também como em alguns casos podemos obter mentalmente as raízes de algumas equações, através da utilização destas relações.
Raízes de uma Equação do 2° grau
Abaixo temos as raízes de uma equação do segundo grau genérica:
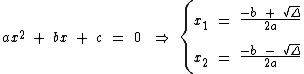
Como já visto em outra página deste site, só existirão raízes reais para a equação, desde que Δ ≥ 0, pois não existe raiz quadrada real de um número negativo.
Soma das Raízes de Equações do 2° grau
Sendo x1 e x2 raízes de uma equação como definido acima, temos que a soma destas raízes será:
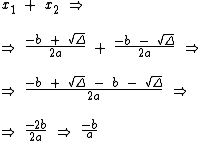
Logo a soma das raízes será dada por:
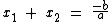
Produto das Raízes de Equações do 2° grau
Assim como no caso da soma, o produto das raízes x1 e x2 será:
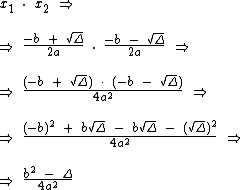
Sabemos que Δ = b2 -4ac. Substituindo-o na equação temos:
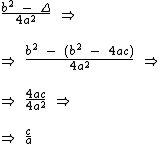
Portanto o produto das raízes será dado por:
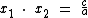
Construção de Equações do 2° grau a partir de suas Raízes
Através da fórmula geral de resolução, também conhecida como fórmula de Bhaskara, partimos de uma equação e chegamos às suas raízes. Agora, com base nas relações de Girard, veremos como a partir das raízes, chegarmos à equação.
A forma reduzida deste tipo de equação é ax2 + bx + c = 0. Realizando a divisão de ambos os membros por a temos:
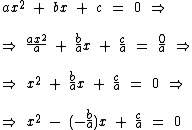
Como supracitado nesta página:
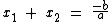
E:
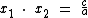
Chamemos de S a soma das raízes ( S = x1 + x2 ) e de P o seu produto ( P = x1 . x2 ). Substituindo na equação temos:
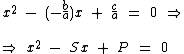
Portanto a equação x2 - Sx + P = 0, onde os coeficientes S e P representam respectivamente a soma e o produto das raízes, nos permite reconstruir a equação que possui estas raízes.
Exemplo
Para a fixação dos conceitos, tomemos uma equação, identifiquemos as suas raízes e a partir delas, através das relações de Girard cheguemos à equação novamente.
 Parta da equação do segundo grau x2 - 5x - 24 = 0, encontre as suas raízes e a partir delas reconstrua a equação original.
Parta da equação do segundo grau x2 - 5x - 24 = 0, encontre as suas raízes e a partir delas reconstrua a equação original.
Em primeiro lugar vamos encontrar as raízes da equação x1 e x2:
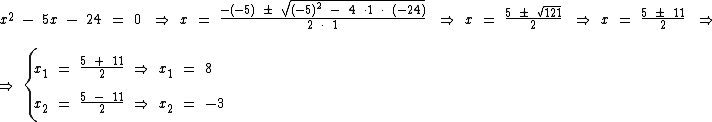
Note que pudemos encontrar duas raízes reais e diferentes para equação, justamente porque Δ > 0. Veja que nesta equação o valor de Δ é 121.
Agora que já conhecemos as suas raízes, através das relações de Girard iremos reconstruir a equação original.
Para a soma das raízes temos:
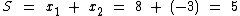
Para o produto das raízes temos:
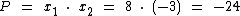
Reconstruindo temos:
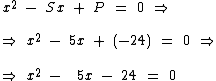
 Portanto partimos da equação x2 - 5x - 24 = 0, encontramos as suas raízes reais x1 = 8 e x2 = -3 e a partir da soma e do produto delas, reconstruímos a equação original.
Portanto partimos da equação x2 - 5x - 24 = 0, encontramos as suas raízes reais x1 = 8 e x2 = -3 e a partir da soma e do produto delas, reconstruímos a equação original.






