Toda equação que contém a incógnita no expoente é denominada equação exponencial.

Vejamos alguns exemplos de equações exponenciais:

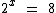
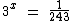
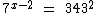
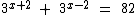
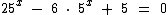
Note que em todas estas equações a incógnita encontra-se no expoente.

Na resolução de equações exponenciais recorremos a muitas das propriedades da potenciação.

Muitas vezes precisamos decompor um número em fatores primos para transformá-lo em uma potência que nos ajudará na resolução da equação.

Em alguns casos, para solucioná-la, transformamos a equação exponencial em uma equação do primeiro grau, em outros as transformamos em uma equação do segundo grau.

Vamos demonstrar como utilizar estes artifícios na resolução das cinco equações exponenciais acima.

Solucionando Equações Exponenciais

Vamos começar com um caso bem simples:

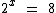
Por experiência própria sabemos que 8 é igual a 2 elevado a 3, então podemos escrever:

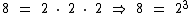
Donde podemos concluir que o valor de x é 3, pois:

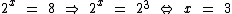
Caso você não se lembre, podemos identificar que 8 é igual a 2³, o decompondo em fatores primos:

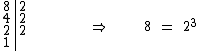
A técnica utilizada para solucionarmos esta equação foi escrever ambos os seus membros na forma de potências de mesma base, no caso a base 2.

Já que as bases são iguais, no conjunto dos números reais as potências serão iguais se e somente se os expoentes também o forem. Mas note que isto só é válido se a base for positiva e diferente de 1. Estudamos sobre o porque desta condição no tópico sobre funções exponenciais.

Agora vamos ao segundo exemplo que é ligeiramente diferente do primeiro:

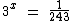
Decompondo o número 243 em fatores primos temos:

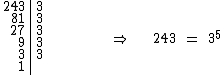
Então temos a seguinte equação com uma potência de 3 no denominador da fração no segundo membro:

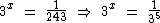
Das propriedades da potenciação sabemos que 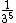é igual a 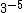, que nos leva ao seguinte:

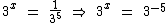
A partir daqui podemos concluir o valor de x da mesma forma que concluímos no exemplo anterior, pois chegamos nos dois membros a potências de mesma base e como a base é maior que zero e diferente de um, podemos concluir que:

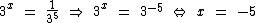
Vamos agora solucionar o terceiro exemplo, que como veremos, também é bastante simples:

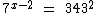
A decomposição do número 343 em fatores primos nos leva a 7³:

O que nos leva a obter a equação:

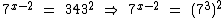
É sabido que podemos multiplicar os expoentes da potência 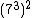, o que resulta em 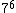, então a equação fica assim:

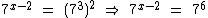
Novamente chegamos em uma situação onde os dois membros da equação são potências de mesma base, portanto a resolveremos como nos casos anteriores, já que 7 é maior que 0 e diferente de 1:

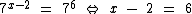
Chegamos então à seguinte equação do primeiro grau:

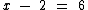
A resolvendo temos:

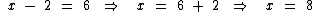
Vamos ver agora um caso um pouco mais complexo:

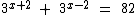
Neste caso de nada adiantará decompormos o número 82 em fatores primos, pois os seus fatores 2 e 41 não nos ajudarão a chegar em uma potência de base 3 como nos termos do primeiro membro, além disto ainda temos uma operação de adição neste membro, que ajuda a complicar um pouco mais a resolução da equação da maneira que vimos até aqui.

Em situações como esta precisamos recorrer a outros artifícios, levando-se em consideração as propriedades da exponenciação.

Note que nesta equação temos dois termos com a incógnita no expoente. Nosso próximo passo é escrever estes termos na forma de um produto no qual um dos fatores seja uma potência com o expoente x, esta potência deverá ser a mesma em ambos os termos.

Já estudamos que na multiplicação de potências de mesma base obtemos como resultado uma potência desta base, cujo expoente é a soma dos expoentes das potências originais:

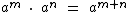
Então se invertermos este raciocínio podemos concluir que a potência 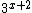pode ser escrita como 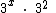, pois ao somarmos x com 2 iremos obter o expoente x + 2:

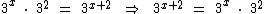
Logo podemos reescrever a nossa equação como a seguir:

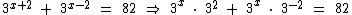
Em vez de trabalharmos com 3^x, podemos trabalhar com y. Então a equação será:

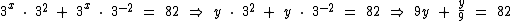
Como chegamos a uma equação do primeiro grau, vamos obter o valor de y solucionando-a:

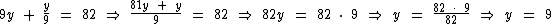
Como y = 3^x temos:

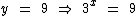
Agora não tem mais segredo, já que a base é positiva e diferente de 1, basta procedermos como nos casos anteriores:

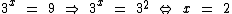
Finalmente vamos ao último caso:

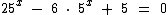
A técnica utilizada será semelhante a do exemplo anterior, só que ao invés de chegarmos a uma equação afim, iremos obter uma equação quadrática:

Note que o primeiro termo 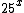pode ser escrito como 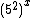, ou como nos convém, escrevê-lo como .

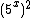Então a equação ficará assim:

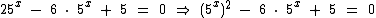
Agora vamos ao artifício de substituir temporariamente 5^x por y:

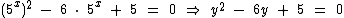
Já que temos uma equação do segundo grau, vamos obter as suas raízes. Para isto podemos recorrer à fórmula geral de resolução, mas neste caso é mais conveniente recorrermos às relações de Albert Girard.

Quais são os dois números reais que somados totalizam 6 e que multiplicados produzem 5?

Obviamente são os números 1 e 5. Estes números são as raízes desta equação.

Se você estiver interessado neste método de resolução de equações quadráticas, por favor, acesse a página equação do segundo grau - calculando facilmente suas raízes para maiores esclarecimentos.

Voltando à vaca fria, como 5^x = y temos: