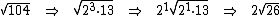Esta calculadora resolve passo a passo equações do segundo grau completas e incompletas, com a seguinte forma:
Nas caixas de texto superiores informe o numerador das frações (a, c, e). Nas inferiores informe os seus denominadores (b, d, f) e nas caixas centrais informe o sinal +/- que as precede.
Com exceção do primeiro termo que não pode ser igual a zero, caso contrário não teríamos uma equação do segundo grau, os demais termos caso sejam iguais a zero devem ser deixados em branco, tanto o termo em si, quanto o operador da linha central.
Você só pode informar números inteiros sem sinal e os denominadores podem ficar em branco, assim como as caixas centrais se for o caso.
 Resolva a equação abaixo:
Resolva a equação abaixo:
Veja a resolução passo a passo da equação do segundo grau
Vamos encontrar os valores numéricos que atribuídos à variável x, tornem verdadeira a seguinte equação:
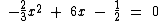
Os valores dos coeficientes a, b e c desta equação são os seguintes:
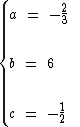
Equação do Segundo Grau Completa
Como temos uma equação do segundo grau completa, iremos calcular o seu discriminante a fim de podermos analisar se ela possui raízes reais ou não.
O discriminante da equação ax2 + bx + c = 0 é representado por: Δ = b2 - 4ac.
Substituindo os coeficientes na fórmula do discriminante temos:
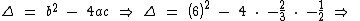
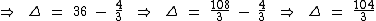
Discriminante maior que zero
Como Δ > 0, a equação tem duas raízes reais e diferentes, pois: 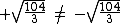
Vamos recorrer à fórmula geral de resolução, vista abaixo, para solucionarmos a equação:
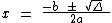
Vejamos:
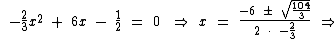
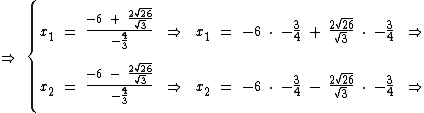
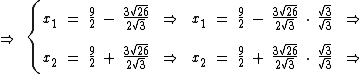
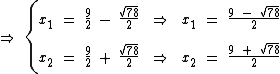
Racionalização do Denominador de uma Fração
Como você deve ter percebido acima, quando tínhamos 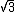 no denominador da fração, a mesma foi multiplicada por uma fração equivalente a 1, com numerador e denominador também iguais a
no denominador da fração, a mesma foi multiplicada por uma fração equivalente a 1, com numerador e denominador também iguais a 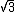 , para que transformássemos o denominador em um número racional, pois como sabemos, a raiz quadrada de um número natural é um número irracional sempre que o radicando não for um quadrado perfeito.
, para que transformássemos o denominador em um número racional, pois como sabemos, a raiz quadrada de um número natural é um número irracional sempre que o radicando não for um quadrado perfeito.
Lembrete sobre a Radiciação do Discriminante
Caso você não se recorde, a radiciação do Δ pode ser tratada através da decomposição em fatores primos como mostrado abaixo, principalmente no caso de números que não são os quadrados perfeitos com os quais você já está familiarizado: