Como já explicado no tópico Equação, equação do 1° grau com duas incógnitas, é qualquer equação que possa ser reduzida à forma ax + by = c, onde x e y são incógnitas e a, b e c são números racionais, com a ≠ 0 e b ≠ 0. a, b e c são coeficientes da equação.

Como também já explicamos no referido tópico, a resolução de problemas de equação do 1° grau com uma incógnita, resume-se a isolarmos a incógnita no primeiro membro, obtendo assim a raiz da equação no segundo membro.

Abaixo temos um exemplo de um problema envolvendo uma equação do 1° grau com duas incógnitas:

"Em minha sapateira tenho sapatos meus e de minha esposa. A sapateira tem capacidade para o armazenamento de 20 pares de sapatos e no momento está lotada. Quantos pares são meus e quantos são de minha esposa?"

Assumindo que a incógnita x represente os meus pares de sapato e que y represente os pares dela, podemos montar a seguinte equação:

x + y = 20

Resolução de equações do 1° grau com duas incógnitas

Antes mesmo de qualquer explicação você pode intuir que a equação x + y = 20 admite várias soluções.

x = 5 e y = 15 é uma das possíveis soluções, já que a soma de 5 com 15 totaliza 20, o que torna a equação verdadeira.

Como a representação de sapatos é realizada pelo conjunto dos números naturais, já que não faria sentido termos sapatos fracionários ou negativos, por exemplo, temos uma solução para qualquer valor de x entre 0 e 20 inclusive, desde que y seja igual a 20 - x, por exemplo, se x = 8, então y = 12.

Matematicamente podemos fazer a seguinte representação:

S = {x, y ∈ N | x ≤ 20, y = 20 - x}

Com x e y sendo números naturais, temos 21 soluções possíveis para este problema, no entanto se não houvesse a restrição para números fracionários ou negativos, teríamos infinitas soluções, pois qualquer que fosse o valor arbitrado a x, bastaríamos subtrair tal valor de 20, para encontrarmos o correspondente valor de y que tornasse a equação verdadeira, por exemplo, se arbitrarmos -30 a x, temos que y = 50, pois 20 - (-30) = 50.

Regra geral para a resolução de equações do primeiro grau com mais de uma variável

Para que você possa obter uma solução para uma equação do primeiro com duas ou mais incógnitas, você deve atribuir um valor aleatório a todas as incógnitas, exceto a uma. Os valores atribuídos devem estar contidos no conjunto universo da equação. A partir daí você terá uma equação do primeiro grau com uma incógnita, cuja solução irá compor a solução da equação original, se o valor encontrado estiver contido no conjunto universo da equação.

Veja este exemplo:

2x + 3y - z = 40 , sendo que o conjunto universo é: U = {x, y, z ∈ N}

Como as incógnitas são números naturais, segundo o seu conjunto universo, só podemos atribuir valores inteiros e positivos às variáveis, ou então o número 0. Podemos então arbitrar 10 a x e 20 a y, para então encontrarmos o valor de z. Vejamos:

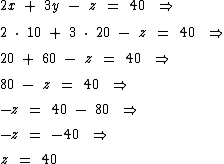
Como 40 ∈ N, então uma dentre as infinitas soluções seria: S = {10, 20, 40}

Agora observe o que aconteceria se tivéssemos arbitrado 3 a x e 5 a y:

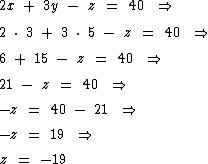
Note que -19 não é um número natural, portanto {3, 5, -19} não está contido no conjunto universo desta equação e por isto não pode ser sua solução.