Toda equação que contém a incógnita na base ou no logaritmando de um logaritmo é denominada equação logarítmica.

Abaixo temos alguns exemplos de equações logarítmicas:

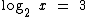
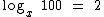
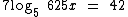
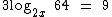
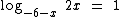
Perceba que nestas equações a incógnita encontra-se ou no logaritmando, ou na base de um logaritmo.

Para solucionarmos equações logarítmicas recorremos a muitas das propriedades dos logaritmos.

Solucionando Equações Logarítmicas

Vamos solucionar cada uma das equações acima, começando pela primeira:

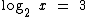
Segundo a definição de logaritmo nós sabemos que:

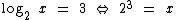
Logo x é igual a 8:

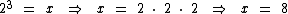
De acordo com a definição de logaritmo o logaritmando deve ser um número real positivo e já que 8 é um número real positivo, podemos aceitá-lo como solução da equação.

A esta restrição damos o nome de condição de existência.

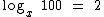
Pela definição de logaritmo a base deve ser um número real e positivo além de ser diferente de 1.

Então a nossa condição de existência da equação acima é que:

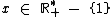
Em relação a esta segunda equação nós podemos escrever a seguinte sentença:

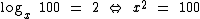
Que nos leva aos seguintes valores de x:

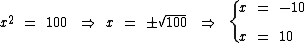
Note que x = -10 não pode ser solução desta equação, pois este valor de x não satisfaz a condição de existência, já que -10 é um número negativo.

Já no caso de x = 10 temos uma solução da equação, pois 10 é um valor que atribuído a x satisfaz a condição de existência, visto que 10 é positivo e diferente de 1.

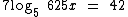
Neste caso temos a seguinte condição de existência:

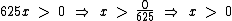
Voltando à equação temos:

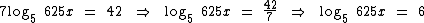
Aplicando a mesma propriedade que aplicamos nos casos anteriores e desenvolvendo os cálculos temos:

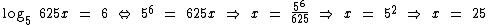
Como 25 satisfaz a condição de existência, então S = {25} é o conjunto solução da equação.

Se quisermos recorrer a outras propriedades dos logaritmos também podemos resolver este exercício assim:

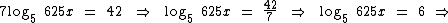
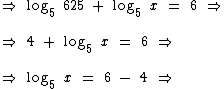
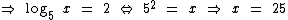
Lembre-se que 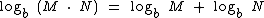e que log₅ 625 = 4, pois 5⁴ = 625.

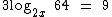
Neste caso a condição de existência em função da base do logaritmo é um pouco mais complexa:

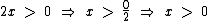
E, além disto, temos também a seguinte condição:

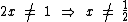
Portanto a condição de existência é:

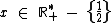
Agora podemos proceder de forma semelhante ao exemplo anterior:

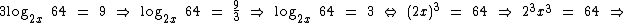
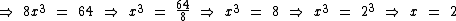
Como x = 2 satisfaz a condição de existência da equação logarítmica, então 2 é solução da equação.

Assim como no exercício anterior, este também pode ser solucionado recorrendo-se à outra propriedade dos logaritmos:

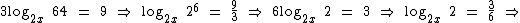
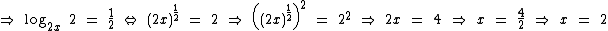
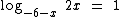
Neste caso vamos fazer um pouco diferente. Primeiro vamos solucionar a equação e depois vamos verificar quais são as condições de existência:

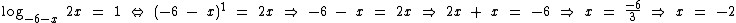
Então x = -2 é um valor candidato à solução da equação.

Vamos analisar as condições de existência da base -6 - x:

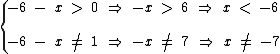
Veja que embora x ≠ -7, x não é menor que -6, portanto x = -2 não satisfaz a condição de existência e não pode ser solução da equação.

Embora não seja necessário, vamos analisar a condição de existência do logaritmando 2x:

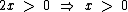
Como x = -2, então x também não satisfaz esta condição de existência, mas não é isto que eu quero que você veja.

O que eu quero que você perceba, é que enquanto uma condição diz que x < -6, a outra diz que x > 0.

Qual é o número real que além de ser menor que -6 é também maior que 0?

Como não existe um número real negativo, que sendo menor que -6, também seja positivo para que seja maior que zero, então sem solucionarmos a equação nós podemos perceber que a mesma não possui solução, já que nunca conseguiremos satisfazer as duas condições simultaneamente.

O conjunto solução da equação é portanto S = {}, já que não existe nenhuma solução real que satisfaça as condições de existência da equação.