Função Exponencial
Aqui no Matemática Didática já tratamos os temas potenciação ou exponenciação e radiciação, como estes são assuntos que têm relação com a função exponencial, é aconselhável que você faça uma breve revisão destes temas, caso não esteja bem familiarizado com eles.
Função exponencial é toda função 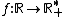 , definida por
, definida por 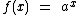 com
com 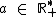 e
e 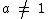 .
.
Neste tipo de função como podemos observar em 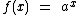 , a variável independente x está no expoente, daí a razão da sua denominação. É importante também observar que a base a é um valor real constante, isto é, um número real.
, a variável independente x está no expoente, daí a razão da sua denominação. É importante também observar que a base a é um valor real constante, isto é, um número real.
Note que temos algumas restrições, visto que temos 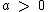 e
e 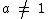 .
.
Se 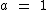 teríamos uma função constante e não exponencial, pois 1 elevado a qualquer x real sempre resultaria em 1. Neste caso
teríamos uma função constante e não exponencial, pois 1 elevado a qualquer x real sempre resultaria em 1. Neste caso 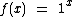 equivaleria a
equivaleria a 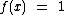 que é uma função constante.
que é uma função constante.
E para 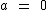 , por que tal restrição?
, por que tal restrição?
Ao estudarmos a potenciação vimos que 00 é indeterminado, então 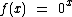 seria indeterminado quando
seria indeterminado quando 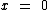 .
.
No caso de 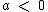 não devemos nos esquecer de que não existe a raiz real de um radicando negativo e índice par, portanto se tivermos, por exemplo,
não devemos nos esquecer de que não existe a raiz real de um radicando negativo e índice par, portanto se tivermos, por exemplo, 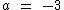 e
e 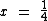 o valor de
o valor de 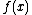 não será um número real, pois teremos:
não será um número real, pois teremos:
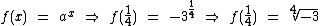
E como sabemos 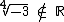 .
.
Representação da Função Exponencial no Plano Cartesiano
Para representarmos graficamente uma função exponencial, podemos fazê-lo da mesma forma que fizemos com a função quadrática, ou seja, arbitrarmos alguns valores para x, montarmos uma tabela com os respectivos valores de f(x), localizarmos os pontos no plano cartesiano e traçarmos a curva do gráfico.
Para a representação gráfica da função 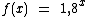 arbitraremos os seguinte valores para x:
arbitraremos os seguinte valores para x:
-6, -3, -1, 0, 1 e 2.
Montando a tabela temos:
| x | y = 1,8x |
|---|
| -6 | y = 1,8-6 = 0.03 |
| -3 | y = 1,8-3 = 0.17 |
| -1 | y = 1,8-1 = 0.56 |
| 0 | y = 1,80 = 1 |
| 1 | y = 1,81 = 1.8 |
| 2 | y = 1,82 = 3.24 |
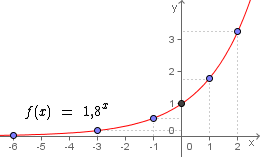
Ao lado temos o gráfico desta função exponencial, onde localizamos cada um dos pontos obtidos da tabela e os interligamos através da curva da função:
Função Crescente e Decrescente
Assim como no caso das funções afim, as funções exponenciais também podem ser classificadas como função crescente ou função decrescente.
Isto se dará em função da base a ser maior ou menor que 1. Lembre-se que segundo a definição da função exponencial 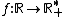 , definida por
, definida por 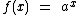 , temos que
, temos que 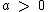 e
e 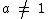 .
.
Função Exponencial Crescente
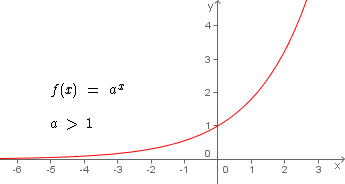
Se 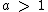 temos uma função exponencial crescente, qualquer que seja o valor real de x.
temos uma função exponencial crescente, qualquer que seja o valor real de x.
No gráfico da função ao lado podemos observar que à medida que x aumenta, também aumenta f(x) ou y. Graficamente vemos que a curva da função é crescente.
Função Exponencial Decrescente
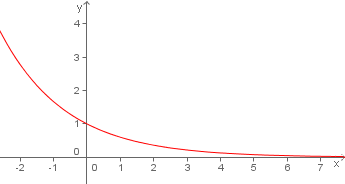
Se 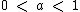 temos uma função exponencial decrescente em todo o domínio da função.
temos uma função exponencial decrescente em todo o domínio da função.
Neste outro gráfico podemos observar que à medida que x aumenta, y diminui. Graficamente observamos que a curva da função é decrescente.
Note também que independentemente de a função ser crescente ou decrescente, o gráfico da função sempre cruza o eixo das ordenadas no ponto (0, 1), além de nunca cruzar o eixo das abscissas.
