Variação de Sinal da Função Polinomial do 2° Grau
Neste tópico vamos fazer o estudo do sinal da função quadrática e como fizemos no estudo da função afim, primeiramente vamos ver como calcular os zeros da função.
Zero ou Raiz da Função Polinomial do 2° Grau
Dada uma função quadrática 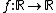 definida por
definida por 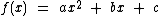 , com
, com 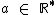 ,
, 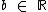 e
e 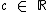 , temos que o zero ou raiz desta função é o valor de x que a anula, isto é, é o valor de x para o qual f(x) = 0, ou em outras palavras, é o valor de x que resulta em y = 0.
, temos que o zero ou raiz desta função é o valor de x que a anula, isto é, é o valor de x para o qual f(x) = 0, ou em outras palavras, é o valor de x que resulta em y = 0.
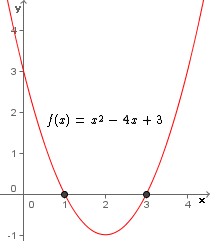
Vamos analisar o gráfico da função 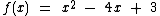 que pode ser visto ao lado:
que pode ser visto ao lado:
Notamos que nos pontos (1, 0) e (3, 0), pertencente ao gráfico da função, temos o valor de x, que é 1 no primeiro ponto e 3 no segundo, anulando a função, isto é, cuja ordenada (y) é igual a zero. Então x = 1 e x = 3 são raízes da função.
No caso da função analisada vimos que a mesma possui duas raízes reais distintas, mas como veremos a seguir, uma função quadrática também pode possuir apenas uma raiz real, ou ainda não possuir qualquer raiz real.
Quando o elemento 0 não pertence ao conjunto imagem da função, esta não possui qualquer raiz, graficamente a parábola na corta o eixo das abscissas.
Quando o elemento 0 pertence ao conjunto imagem da função e todos os demais elementos da imagem são positivos ou todos os demais elementos são negativos, então a parábola apenas tangencia o eixo das abscissas e por isto a função tem somente uma raiz real.
Determinando as Raízes de uma Função Polinomial do 2° Grau
Vamos determinar algebricamente a raiz da função 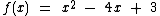 cujo gráfico temos acima.
cujo gráfico temos acima.
Para que um valor x seja raiz da função, é necessário que f(x) = 0.
Realizando tal substituição na lei de formação da função temos:
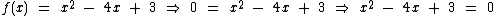
Como a equação encontrada é uma equação do segundo grau, para determinarmos os valores de x que são raízes da função, basta encontrarmos as raízes desta equação:
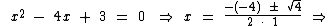
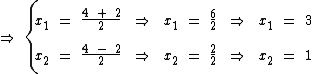
Como era previsto, 3 e 1 são os valores de x que tornam y = 0. No gráfico os pontos (1, 0) e (3, 0) são os pontos representantes das raízes desta função.
Em resumo para encontrarmos as raízes de uma função quadrática basta substituirmos o f(x) ou y da lei de formação da função, por 0 e solucionarmos a equação do segundo grau encontrada, chegando assim às raízes da função, obviamente se existirem.
Estudo do Sinal de uma Função Quadrática
Estudar a variação do sinal de uma função polinomial do 2° grau é identificar para quais valores de x temos f(x) com valor negativo, nulo ou positivo.
Generalizando o Estudo da Variação do Sinal de uma Função Quadrática
Como vimos acima para realizarmos o estudo da variação do sinal de uma função quadrática precisamos conhecer as suas raízes e também se a parábola tem a sua concavidade voltada para cima ou para baixo.
Ao iniciarmos os estudos das funções polinomiais do 2° grau vimos que a direção da concavidade da parábola depende diretamente do coeficiente a da sua regra de associação.
Em função das raízes da função e da direção da concavidade da parábola temos seis possíveis situações distintas:
Função com Duas Raízes Reais e Concavidade Voltada para Cima
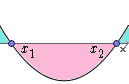
Neste caso temos duas raízes reais distintas x1 e x2, sendo x1 < x2.
A parábola corta o eixo das abscissas em dois pontos.
Temos o seguinte estudo da variação do sinal da função:
 A função é negativa para
A função é negativa para 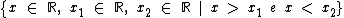 .
.
 A função é nula para
A função é nula para 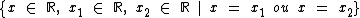 .
.
 A função é positiva para
A função é positiva para 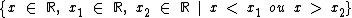 .
.
Função com Duas Raízes Reais e Concavidade Voltada para Baixo
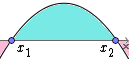
Neste caso também temos duas raízes reais distintas x1 e x2, sendo x1 < x2.
A parábola igualmente corta o eixo das abscissas em dois pontos distintos.
Neste e no caso anterior temos que Δ > 0.
Estudando a variação do sinal da função temos:
 A função é negativa para
A função é negativa para 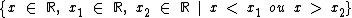 .
.
 A função é nula para
A função é nula para 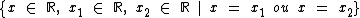 .
.
 A função é positiva para
A função é positiva para 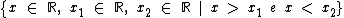 .
.
Função com Uma Raiz Real e Concavidade Voltada para Cima
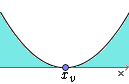
Nesta situação temos apenas uma raiz real xv que é a abscissa do vértice da parábola.
A parábola apenas tangencia o eixo das abscissas.
Temos o seguinte estudo da variação do sinal da função:
 A função é nula para
A função é nula para 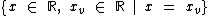 .
.
 A função é positiva para
A função é positiva para 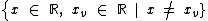 .
.
Função com Uma Raiz Real e Concavidade Voltada para Baixo
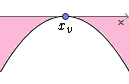
Nesta outra situação também temos apenas uma raiz real xv correspondente a abscissa do vértice da parábola.
A parábola novamente apenas tangencia o eixo das abscissas.
Neste e no caso acima temos que Δ = 0.
O estudo da variação do sinal da função é o seguinte:
 A função é nula para
A função é nula para 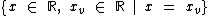 .
.
 A função é negativa para
A função é negativa para 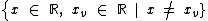 .
.
Função sem Raízes Reais e Concavidade Voltada para Cima
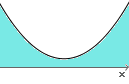
Agora não temos qualquer raiz real.
A parábola não corta nem tangencia o eixo das abscissas em nenhum ponto.
O estudo da variação do sinal da função é então:
 A função é positiva para
A função é positiva para 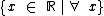 .
.
Função sem Raízes Reais e Concavidade Voltada para Baixo
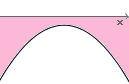
No sexto e último caso também não temos nenhuma raiz real.
A parábola igualmente não corta nem tangencia o eixo das abscissas em nenhum ponto.
Neste e no caso anterior temos que Δ < 0, além disto nestes casos o sinal a função é sempre igual ao sinal do coeficiente a.
O estudo da variação do sinal da função é:
 A função é negativa para
A função é negativa para 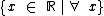 .
.
