Função Par

Denominamos função par uma função f, quando para todo elemento x pertencente ao domínio da função temos f(x) = f(-x).

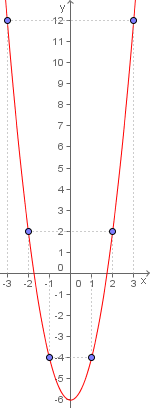
Vamos analisar a função 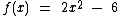cuja representação gráfica temos ao lado.

Vamos começar pelo lado direito do eixo das ordenadas.

Veja que para x igual a 1, 2 ou 3, temos y igual a -4, 2 ou 12, respectivamente.

Isto porque:

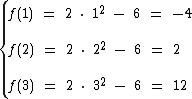
Agora vamos analisar o lado esquerdo do eixo das ordenadas.

Note que para x igual a -1, -2 e -3, temos y igual aos mesmos -4, 2 e 12, respectivamente.

Evidentemente porque:

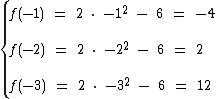
Qualquer que seja x temos f(x) = f(-x):

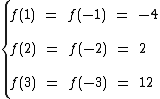
Portanto 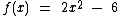é uma função par.

Visto que f(x) = f(-x), então x e o seu oposto -x possuem a mesma imagem.

Como você já deve ter percebido, o gráfico de uma função par é simétrico em relação ao eixo das ordenadas, isto é, o lado direito espelha o esquerdo e vice-versa.

Função Ímpar

Denominamos função ímpar uma função f, quando para todo elemento x pertencente ao domínio da função, temos f(x) = -f(-x), que também podemos escrever como -f(x) = f(-x).

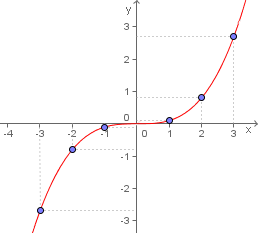
Vamos analisar a função 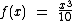representada pelo gráfico ao lado.

Podemos notar que o gráfico é simétrico em relação à origem do plano cartesiano.

Observe que os pontos para os quais x é igual a 1, 2 ou 3, estão localizados em posição simétrica à partir da origem, em relação aos pontos para os quais x é igual a -1, -2 ou -3, respectivamente.

Para termos o valor exato das imagens, primeiramente vamos calcular f(x) para x igual a 1, 2 e 3:

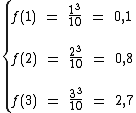
Ainda para x igual a 1, 2 e 3 vamos calcular -f(-x) para podermos fazer uma comparação:

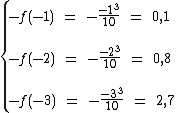
Veja que f(x) = -f(-x):

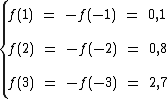
Visto que -f(x) = f(-x), então x e o seu oposto -x têm imagens opostas.

Funções que não são Par nem Ímpar

No casos dos números naturais quando um número não é par ele só pode ser ímpar e vice-versa.

No caso de funções a coisa não é bem assim que funciona.

Para que uma função seja denominada função par ou função ímpar, é preciso que a mesma se enquadre exatamente nas condições impostas vistas acima.

Acontece que existem funções que não satisfazem nem a condição para serem denominadas funções pares, nem tampouco para serem denominadas funções ímpares.

Vejamos o caso da função 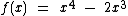no gráfico ao lado.

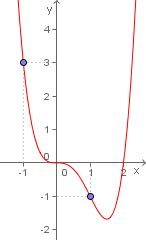
Como podemos observar, não existe a simetria visual vistas nos gráficos anteriores, nem quanto a uma função par, nem quanto a uma função ímpar.

No caso função par teríamos f(x) = f(-x), ou seja, as imagens de x = 1 e de x = -1, por exemplo, deveriam ser iguais, mas pelo gráfico e pelos cálculos realizados abaixo vemos que isto não ocorre:

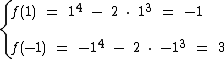
Então 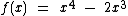não é uma função par.

Para que ela fosse uma função ímpar teríamos -f(x) = f(-x), ou seja, as imagens de x = 1 e de x = -1, por exemplo, deveriam ser opostas uma da outra, mas pelo gráfico e pelos cálculos realizados acima vemos que isto também não ocorre:

Portanto 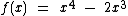também não é uma função ímpar.