No Matemática Didática temos um artigo no qual estudamos em maiores detalhes as taxas nominais, efetivas e equivalentes. Neste "O xis da questão" temos um exercício as envolvendo, no qual a partir de uma taxa nominal pretendemos obter a taxa efetiva anual:
Em função da minha dificuldade financeira em quitar uma dívida no cheque especial, meu gerente propôs a mim um empréstimo a uma taxa 35,4% a.a., com capitalização bimestral. Qual a taxa anual efetiva deste empréstimo?
Note no enunciado que a proposta do gerente se refere a uma taxa a.a., no entanto os juros são acrescidos ao capital a cada bimestre. Trata-se, portanto, de uma taxa nominal, a taxa de 35,4% a.a., pois o período de formação e acréscimo dos juros ao principal, é diferente do período de tempo da taxa de juros.
Como os juros serão capitalizados a cada bimestre, precisamos conhecer a taxa efetiva ao bimestre. Para obtê-la basta dividirmos a taxa de 35,4%, que é anual, pelo número de bimestres em 1 ano:
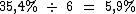
Agora sabemos que os juros serão acrescidos a cada bimestre a um taxa efetiva de 5,9% a.b.
Como o enunciado do problema pede uma taxa anual efetiva, prescisamos calculá-la através da seguinte expressão:
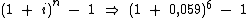
O número 0,059 se refere à taxa efetiva de 5,9% a.b. na sua forma decimal, resultado da divisão de 5,9 por 100.
O expoente 6 é o número de bimestres em um ano, resultante da divisão do número de meses em um ano pelo número de meses em um bimestre.
Concluindo as operações temos:
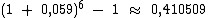
0,410509 é o valor aproximado desta expressão. Ela já representa a taxa anual efetiva, mas na sua forma decimal. Para convertê-la para a forma percentual basta que a multipliquemos por 100%:
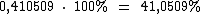
As taxas de 5,9% a.b. e 41,0509% a.a. são taxas equivalentes, isto porque o montante obtido ao aplicarmos um capital à taxa de 5,9% a.b. por 6 bimestres, será o mesmo montante resultante da aplicação deste capital durante 1 ano pela taxa de 41,0509% a.a.
Para a confirmação disto vamos realizar uma simulação para um capital de R$ 10.000,00.
Para a taxa de 5,9% a.b. durante 6 bimestres temos:
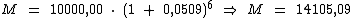
Já para a taxa de 41,0509% a.a. pelo período de 1 ano temos:
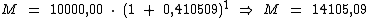
Note que calculamos a taxa de 41,0509% a.a. com uma aproximação de 4 casas decimais apenas para que os montantes resultassem exatamente em R$ 14.105,09 nesta nossa demonstração, senão haveria uma pequena diferença de centavos, mas na prática podemos trabalhar apenas com duas casas decimais, como 41,05% a.a., ou até com nenhuma, dependendo da precisão desejada.
A taxa anual efetiva deste empréstimo é de 41,05% a.a.
