Neste "O xis da questão" temos um problema que pode ser solucionado criando um sistema com duas equações e duas variáveis.
Primeiro vemos como equacioná-lo e depois como chegarmos à sua solução.
Dois caminhões estão sendo carregados à razão de 6 caixas por minuto. Já colocaram 300 caixas no primeiro caminhão e no segundo apenas 60. Em quanto tempo o primeiro caminhão conterá o triplo de caixas do segundo?
Vamos representar pela letra t a variável que indica o tempo necessário para que o primeiro caminhão passe a conter o triplo de caixas do segundo caminhão. A quantidade de caixas em um dado momento representemos pela letra c.
Inicialmente o segundo caminhão contém uma carga de 60 caixas, que aumenta em 6 caixas a cada minuto:
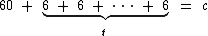
Logo, a carga no segundo caminhão pode ser assim equacionada:
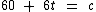
Em relação ao primeiro caminhão, inicialmente ele contém uma carga de 300 caixas que aumenta à razão 6 caixas por minuto. Como a sua carga deve ser o triplo da carga do segundo, temos que:
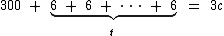
Logo, a equação da carga no primeiro caminhão será:
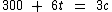
Como temos duas equações e duas variáveis, podemos montar um sistema de equações do primeiro grau com duas incógnitas para encontrarmos o valor da variável t, que é a incógnita que nos interessa:
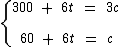
Podemos solucioná-lo pelo método da adição, multiplicando a segunda equação por -3 e somando com a primeira, assim eliminamos a variável c e identificamos o valor numérico de t:
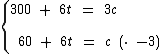
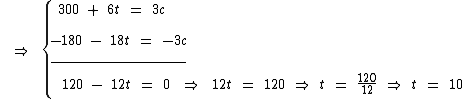
Portanto, em 10 minutos a quantidade de caixas no primeiro caminhão será três vezes maior que a quantidade de caixas no segundo caminhão.
De fato, em 10 minutos cada caminhão será carregado com mais 60 caixas.
Como o primeiro já continha 300 caixas, irá conter 360:
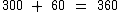
Visto que o segundo caminhão continha 60 caixas, com mais 60 irá conter 120:
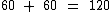
Como podemos observar, 360 é o triplo de 120:
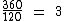
Em 10 minutos o primeiro caminhão irá conter o triplo de caixas do segundo.
