É bastante comum questões sobre probabilidade darem um nó na cabeça de muitos estudantes, principalmente se envolverem mais de um evento, sejam eles independentes, ou não.
Com o objetivo de auxiliá-los nesta matéria, este é o tema tratado neste "O xis da questão":
Maria tem 70% de chances de viajar nas férias de final de ano. Jéssica tem apenas 20% de chances de viajar nestas férias. Sendo que elas tomarão a decisão de viajar independentemente uma da outra, qual é a probabilidade de que ao menos uma delas viaje?
Como é comum fazermos algumas vezes, vamos solucionar este problema de duas maneiras. Para começar vamos utilizar o método mais simples e mais rápido.
O objetivo da questão é descobrir qual é a probabilidade de que ao menos uma das mulheres viaje, ou seja, pode ser que viaje apenas uma delas ou que viajem as duas.
Em problemas com as características deste é mais fácil calcularmos a probabilidade de nenhuma delas viajar e depois calcularmos a probabilidade complementar, que será o percentual que estamos procurando.
A probabilidade de Maria viajar ou não, é de 100%, ou seja, ou ela viaja (probabilidade de 70%), ou ela não viaja (probabilidade de 30%):
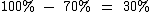
De forma análoga, a probabilidade de Jéssica não viajar é de 80%:
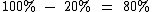
A probabilidade das duas não viajarem é igual ao produto da probabilidade individual de cada uma delas não viajar:
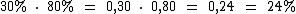
Ora, se a probabilidade de ambas não viajarem é de 24%, a probabilidade de ao menos uma delas viajar é a probabilidade complementar disto:
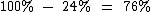
Uma outra forma de resolvermos este problema é calcularmos a probabilidade da união de dois eventos independentes, que como já vimos, pode ser obtida através da seguinte fórmula:
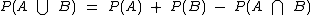
Chamemos de P(A) e P(B) as respectivas probabilidades de Maria e Jéssica viajarem.
A probabilidade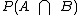 
, que é a probabilidade da intersecção de dois eventos independentes de um mesmo espaço amostral, é resultado do produto de P(A) por P(B):
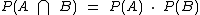
Dito isto, podemos realizar os cálculos da probabilidade em questão:
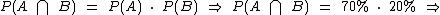
Substituindo as probabilidades conhecidas na fórmula acima, temos:
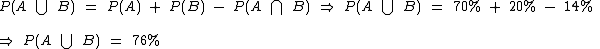
Note que obtivemos o mesmo resultado anterior.
Agora vamos raciocinar um pouco:
Caso você não tenha percebido,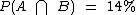 
é a probabilidade de as duas mulheres viajarem.
Como a probabilidade de Maria viajar é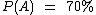 
, independentemente de Jéssica viajar, ou não. Se a probabilidade das duas viajarem é de 14%, então a probabilidade de somente Maria viajar é 56%:
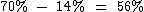
Analogamente, a probabilidade de somente Jéssica viajar é 6%:
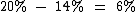
A probabilidade de ao menos uma delas viajar (só Maria viajar, só Jéssica, ou as duas viajarem), é dada pela soma destas três probabilidades:
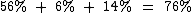
É por isto que subtraímos 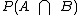, senão estaríamos somando o 14% duas vezes:
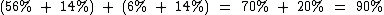
Que incorreria em um resultado errôneo de 90% e não de 76% que é a solução correta.
Divagando um pouco, note que neste artigo apresentamos duas formas que podemos utilizar quando precisamos multiplicar porcentagens. Você pode usar qualquer um dos métodos. O segundo é mais simples e direto, ao utilizarmos este método não convertemos a última porcentagem para a forma decimal ou fracionária, só as porcentagens anteriores.
A probabilidade de que ao menos uma delas viaje nas férias de final de ano é de 76%.
