Exercícios Simulados Resolvidos
Primeiro Simulado Matemática Didática
Resolva as Questões Abaixo:
1) Um certo produto teve um reajuste de preço de 20%. Como o mercado não se sujeitou a este novo valor, qual deve ser o percentual de desconto a ser dado no valor atual, que equivalha a 5% de aumento no preço original do produto?
2) Dois ciclistas estão a dar voltas em torno de um parque ecológico. Um dos ciclistas dá uma volta completa em 40 minutos e o outro completa uma volta em uma hora. Ao meio-dia eles estavam no mesmo ponto. Em qual horário eles voltaram a se encontrar novamente neste referido ponto?
3) Se eu deixar R$ 10.000,00 aplicados por 2 anos, qual deverá ser a taxa de juro composto mensal para que ao final deste período eu resgate o triplo deste valor?
4) Em uma prova João fez três pontos a mais que Paulo, que fez seis pontos a mais que Luís. A média aritmética das notas dos três é seis. Quantos pontos fez cada um?
5) Três amigos, em uma lanchonete, dividiram uma despesa de R$ 144,00 em partes diretamente proporcionais ao número de refrigerantes que cada um deles tomou. O primeiro tomou três refrigerantes, o segundo tomou quatro e o terceiro tomou cinco. Quanto pagou cada um deles respectivamente?
6) Quantos divisores naturais possui o número 500?
7) A soma de dois números é igual a 168. Sabe-se que um deles está para 3, assim como o outro está para 5. Quais são estes números?
8) Pretendo ter um aumento salarial de 20%, de sorte que a soma do meu salário atual com o salário reajustado totalize R$ 3.300,00. Quanto eu recebo atualmente?
9) Trabalhando duas horas por dia, três vezes por semana, eu produzo 60 itens de artesanato. Trabalhando três horas por dia, cinco vezes por semana, conseguirei produzir quantos itens?
10) Qual o valor da prestação de um produto que à vista custa R$ 1.310,00, pago em 1+2 vezes, com uma taxa de juros mensal de 1,8% a.m.?
Resolução Detalhada das Questões do Simulado
Resolução da Primeira Questão:
Digamos que o preço original deste produto seja igual a x. Neste caso podemos afirmar que o preço do produto reajustado será igual a 1,2x. Vejamos:
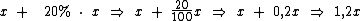
Pelo mesmo raciocínio podemos afirmar que se o produto tivesse sido reajustado em 5%, seu novo valor seria 1,05x:
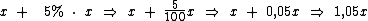
A diferença entre os preços com reajuste de 20% e com reajuste de 5% é:
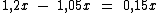
Ou seja, 0,15x é o valor do desconto que deve ser dado sobre o preço reajustado em 20%, para que equivalha a um reajuste de 5% sobre o preço original. Resta-nos então saber quantos por cento de 1,2x equivalem a 0,15x. Vejamos:
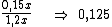
Para que tenhamos a resposta na forma de porcentagem, basta multiplicarmos 0,125 por 100 e inserirmos o símbolo "%" à sua direita: 12,5%.
Portanto:
d é a alternativa correta.
Resolução da Segunda Questão:
Ao completar cada volta, para que saibamos há quanto tempo o ciclista está pedalando, basta que multipliquemos o número de volta executadas, pelo número de minutos que ele demora a executar cada volta.
Em outras palavras este tempo é múltiplo de 40, ou de 60 minutos dependendo do ciclista.
O problema se resume então em se identificar qual é o menor múltiplo comum entre 40 e 60, isto é o MMC(40,60).
Utilizando-se da nossa calculadora para o cálculo de MMC/MDC, você poderá passo a passo verificar os cálculos realizados para apuramos que o MMC(40, 60) = 120.
Como 120 minutos equivalem a 2 horas, então os ciclistas se encontrarão às 14:00, quando então o ciclista com menor ritmo completará 2 voltas e o outro completará 3 voltas.
Portanto:
b é a alternativa correta.
Resolução da Terceira Questão:
Como o valor a receber deve ser de R$ 30.000,00, o triplo do valor aplicado, então temos as seguintes variáveis para a obtenção da taxa de juro composto:
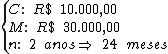
Substituindo o valor das variáveis na fórmula abaixo temos:
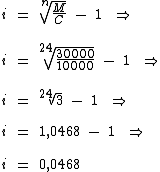
0,0468 na sua forma decimal, multiplicado por cem corresponde a 4,68% na forma de porcentagem.
Portanto:
c é a alternativa correta.
Resolução da Quarta Questão:
Chamemos João, Paulo e Luís de J, P e L. A partir do enunciado podemos abstrair as seguintes equações:
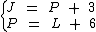
Trocando P por L + 6 na primeira expressão temos:
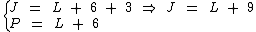
Como enunciado diz que a média aritmética das três notas é seis, temos:
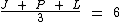
Substituindo as variáveis J e P temos:
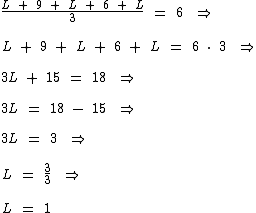
Substituindo a variável L nas expressões abaixo temos:
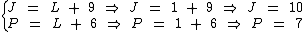
Logo João fez 10 pontos, Paulo fez 7 pontos e Luís fez 1 ponto.
Portanto:
e é a alternativa correta.
Resolução da Quinta Questão:
Conforme as explicações no tópico Divisão em Partes Diretamente Proporcionais, a partir do enunciado montamos as seguintes expressões:
- p1 = K . 3
- p2 = K . 4
- p3 = K . 5
- p1 + p2 + p3 = 144
Para encontrarmos o valor da constante K devemos substituir o valor de p1, p2 e p3 na última expressão:
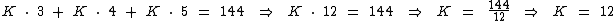
Logo:
- p1 = 12 . 3 = 36
- p2 = 12 . 4 = 48
- p3 = 12 . 5 = 60
De onde concluímos que o primeiro pagou R$ 36,00, o segundo pagou R$ 48,00 e R$ 60,00 foi o valor pago pelo terceiro.
Portanto:
a é a alternativa correta.
Resolução da Sexta Questão:
Decompondo o número natural 500 em fatores primos, conforme o explicado no tópico Decomposição de um Número Natural em Fatores Primos temos que: 500 = 22 . 53.
Agora segundo o explicado no tópico Divisores de um Número Natural sabemos que para obtermos todos os divisores naturais de 500, devemos acrescentar uma unidade a cada um dos expoentes dos seus fatores primos e multiplicá-los. Vejamos:
Os expoentes são 2 de 22 e 3 de 53. Logo temos:
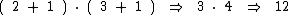
Ou seja, 500 possui 12 divisores naturais.
Portanto:
c é a alternativa correta.
Resolução da Sétima Questão:
Para a resolução deste exemplo utilizaremos a terceira propriedade das proporções. Para maiores informações sobre este assunto acesse o tópico Proporção.
Chamando um dos números de a e o outro de b, podemos montar a seguinte proporção:
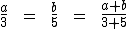
Sabemos que a soma de a com b resulta em 168, assim como a adição de 3 a 5 resulta em 8. Substituindo estes valores na proporção teremos:
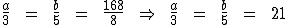
Portanto:
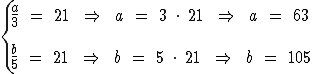
Concluímos então que os dois números são 63 e 105.
Portanto:
e é a alternativa correta.
Resolução da Oitava Questão:
Assumindo que o meu salário atual seja igual a x, o meu salário reajustado será:
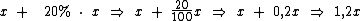
Sei que o meu salário atual (x), acrescentado do salário reajustado (1,2x) totaliza R$ 3.300,00. Podemos então montar a seguinte equação do primeiro grau:
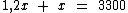
Resolvendo a equação encontraremos o salário atual:
Logo o meu salário atual é de R$ 1.500,00.
Portanto:
b é a alternativa correta.
Resolução da Nona Questão:
Para realizarmos os cálculos vamos atribuir uma letra a cada uma das grandezas do problema:
- H: A quantidade de horas trabalhadas por dia;
- S: A quantidade de dias trabalhados por semana;
- I: O número de itens produzidos.
A partir dos dados do enunciado montamos a seguinte representação para a análise do problema:
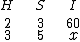
Como na montagem a grandeza procurada (I) esta à esquerda das outras, facilmente poderemos isolá-la das demais.
Agora vamos determinar se as grandezas são diretamente ou inversamente proporcionais à grandeza I. Para isto utilizaremos setas com a mesma orientação para indicar grandezas diretamente proporcionais e com orientação inversa para indicar o oposto.
Vamos arbitrar que a orientação da grandeza I seja para baixo:
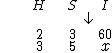
Agora vejamos se I e H são diretamente proporcionais ou não. Sabemos que ao aumentarmos a quantidade de horas trabalhadas por dia, também iremos aumentar a quantidade de itens produzidos, sendo assim as duas grandezas são diretamente proporcionais, então a seta de H terá a mesma orientação da seta de I que é para baixo:
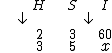
Determinemos se I e S são diretamente ou inversamente proporcionais. Ao aumentarmos o número de dias trabalhados por semana, também iremos aumentar a quantidade de itens produzidos, isto nos mostra que as duas grandezas são diretamente proporcionais, então a seta de S será orientada para baixo, assim como a seta de I:
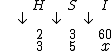
Como todas as grandezas têm a mesma orientação não precisamos realizar nenhuma inversão (todas as grandezas são proporcionais entre si), resta-nos então montar a proporção e resolvê-la:
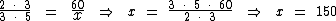
Ou seja, trabalhando três horas por dia, cinco vezes por semana, conseguirei produzir 150 itens.
Portanto:
a é a alternativa correta.
Resolução da Décima Questão:
Para o cálculo do valor das prestações com o mesmo valor da entrada, iremos utilizar esta fórmula:
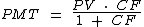
A partir do enunciado identificamos os seguintes valores para as variáveis:
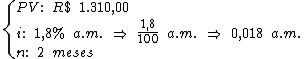
Note que o período de financiamento é de apenas dois meses, pois o valor da entrada não sofre a incidência de juros.
Para utilizarmos a fórmula acima, precisamos obter o coeficiente de financiamento. Seu cálculo é realizado abaixo:
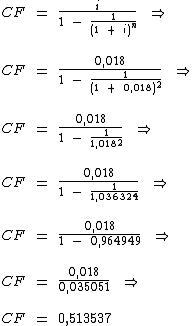
Substituindo-se os valores das variáveis na fórmula da prestação com entrada de igual valor:
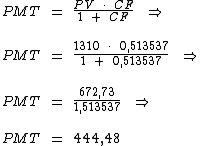
Portanto:
d é a alternativa correta.
