Exercícios Simulados Resolvidos
Segundo Simulado Matemática Didática
Resolva as Questões Abaixo:
1) Em um estacionamento há carros e motos. O número de motos é o triplo do número de carros. Somando-se o número de pneus, obtemos 60. Qual é o número de carros e de motos neste estacionamento? Os estepes não são considerados.
2) Em um armário cabem exatamente, sem sobrar espaço vazio, 24 caixas pequenas, ou 12 caixas grandes. Se nele eu colocar 5 caixas das grandes, quantas ainda poderei colocar das pequenas para ocupar todo o espaço restante?
3) Estou fazendo uma viagem de moto e já percorri 5/17 do trajeto, tendo consumido de 5 litros de combustível. Quantos reais gastarei para fazer todo o percurso, sabendo-se que o litro do combustível custa R$ 3,00?
4) Em 2009 eu e meu irmão tínhamos respectivamente 45 e 40 anos. Em qual ano a minha idade era dobro da dele?
5) Juntos Xavier e Yuri possuem 20 carrinhos, no entanto Xavier possui 4 carrinhos a mais que Yuri. Quantos carrinhos possuem respectivamente Xavier e Yuri?
6) A soma de quatro números consecutivos é igual a 74. Qual seria o próximo número da sequência para termos cinco números consecutivos?
7) Em uma empresa os seus três vendedores receberam uma certa quantidade de brindes a serem distribuídos aos seus clientes. O primeiro recebeu 3/7 do total, mais 10 unidades. O segundo 1/6 do total, menos 5 unidades. O terceiro ficou com os 80 brindes restantes. Quantos eram os brindes no total?
8) Para a festinha de meu filho mandei comprar 4 dúzias de suco e 3 dúzias de refrigente, o que me custou R$ 258,00. Se ao invés das 3 dúzias, eu tivesse comprado 2 dúzias de refrigerante, eu teria gasto R$ 228,00. Qual o preço unitário do suco?
9) Numa festinha de crianças, 300 docinhos iriam ser divididos igualmente entre as 50 crianças presentes, mas por um motivo qualquer todos os meninos foram embora mais cedo, então os docinhos foram repartidos em partes iguais entre as meninas, que acabaram ganhando 9 doces a mais do que iriam ganhar inicialmente. Quantas eram as meninas e quantos eram os meninos?
10) Um doceiro torrou amendoins para serem vendidos na porta de uma escola e os colocou em saquinhos de 50 gramas. Se tivesse usado saquinhos de 80 gramas, teria dado para 21 saquinhos a menos. Quantos gramas de amendoim ele torrou?
Resolução Detalhada das Questões do Simulado
Resolução da Primeira Questão:
Para a resolução deste problema iremos recorrer a álgebra. Recorrendo a álgebra iremos montar equações onde os valores desconhecidos serão substituídos por letras. Como desconhecemos o número de motos e de carros, iremos utilizar a letra "m" para representar as motos e a letra "c" para representar os carros.
O enunciado diz que o número de motos é o triplo do número de carros. Podemos então escrever a seguinte equação:
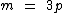
O enunciado também nos diz que 60 é o número total de pneus no estacionamento. Como sabemos que as motos possuem 2 pneus e os carros possuem 4, podemos montar a seguinte equação:
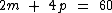
Esta equação indica que o número de motos multiplicado pelo número de pneus que elas possuem, somado ao número de carros multiplicado pelo número de pneus dos mesmos, é igual ao número total de pneus no estacionamento.
Sabemos que m é igual a 3p, então vamos substituir m por 3p na segunda equação:
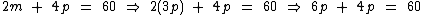
Agora iremos isolar a incógnita p no primeiro membro, para obtermos o total de carros no estacionamento:
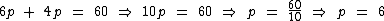
Já descobrimos que 6 é a quantidade de carros, para descobrimos a quantidade de motos, basta substituirmos na primeira equação, p pelo seu valor numérico:
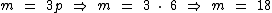
Portanto:
c é a alternativa correta.
Resolução da Segunda Questão:
Neste tipo de problema você deve encontrar a fração do armário que ainda não foi ocupada. Como o armário todo comporta até 12 caixas das grandes e só foram colocadas nele 5 caixas deste tipo, então ainda há espaço para 7 caixas das grandes:
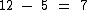
Logo a fração do armário que ainda não foi utilizada é de 7 em 12, ou seja:
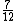
Por fim, resta-nos calcular quanto é sete doze avos das 24 caixas pequenas:
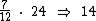
Assim sendo:
d é a alternativa correta.
Resolução da Terceira Questão:
Como já houve um consumo de 5 litros de combustível, o gasto até então foi de quinze reais, já que três reais é o preço do litro:
Se soubéssemos a quantia total gasta para fazer o percurso e a multiplicássemos por 5/17 referente à distância percorrida, iríamos obter os R$ 15,00 referentes ao consumo dos cinco litros. Como sabemos os R$ 15,00, mas não a quantia total, basta fazermos a conta inversa, ou seja dividirmos R$ 15,00 por 5/17:
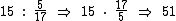
Portanto:
a é a alternativa correta.
Resolução da Quarta Questão:
Neste exercício temos que subtrair de ambas as idades um valor desconhecido que chamaremos de x, tal que a divisão da minha idade na época pela do meu irmão, seja igual a dois. Podemos então montar a seguinte equação:
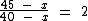
Resolvendo a equação temos:
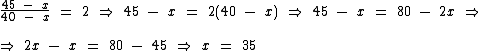
Então 35 anos atrás a minha idade era o dobro da idade do meu irmão, de fato naquela época eu estava com 10 anos e ele com 5 anos, ou seja, a minha idade era o dobro da dele.
Se o ano de referência é 2009, então 35 anos atrás era o ano de 1974:
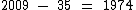
Logo:
e é a alternativa correta.
Resolução da Quinta Questão:
Vamos solucionar este exercício de duas formas distintas. Primeiro simplesmente através de cálculos aritméticos e depois através da álgebra, mais especificamente através da resolução de sistemas lineares.
Se desconsiderarmos os 4 carrinhos que Xavier possui a mais que Yuri, juntos eles terão 16 carrinhos:
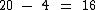
Neste caso possuirão a mesma quantidade de carrinhos, cada um terá a metade deles, ou seja, cada um terá 8 carrinhos:
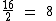
No entanto como Xavier possui 4 carrinhos a mais, ele possuirá 12 carrinhos e Yuri apenas 8:
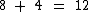
Na solução algébrica atribuiremos a Xavier a incógnita x e a Yuri a incógnita y.
Como juntos eles possuem 20 carrinhos, temos:
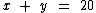
Como Xavier tem 4 carrinhos a mais, temos:
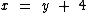
Substituindo x na primeira equação por y + 4, conforme a segunda equação temos:
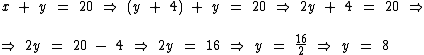
Substituindo y por seu valor na segunda equação:
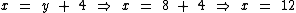
Como apurado anteriormente através de cálculos aritméticos, temos que Xavier possui 12 carrinhos e que Yuri possui os outros 8.
Portanto:
b é a alternativa correta.
Resolução da Sexta Questão:
Pensando em termos aritméticos, o segundo número da sequência é igual ao primeiro acrescentado de uma unidade, o terceiro é igual ao primeiro acrescentado de duas unidades e quarto é igual ao primeiro acrescentado de três unidades.
Então no total foram somadas seis unidades, uma no segundo mais duas no terceiro e mais três no quarto. Se não tivessem ocorrido tais acréscimos, todos os quatro números seriam iguais e a soma seria igual a 68:
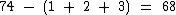
Dividindo 68 por 4 iremos encontrar o valor do primeiro número da série:
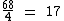
Como o primeiro número da sequência é igual a dezessete, o quinto número da série será igual ao primeiro acrescentado de quatro unidades:
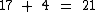
Pensando em termos algébricos, se representarmos o primeiro número pela letra x, podemos montar a seguinte equação:
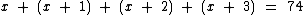
Teremos o primeiro número ao encontrarmos o valor de x:
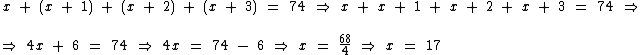
Somando então 4 a 17 iremos novamente encontrar o valor do quinto número da sequência.
Então:
d é a alternativa correta.
Resolução da Sétima Questão:
Chamemos de x a quantidade total de brindes na empresa a ser distribuída. Podemos então montar a seguinte equação algébrica:
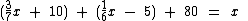
Esta equação nos mostra que a soma de todas as quantidades recebidas pelos vendedores é igual a quantidade total de brindes. Basta resolvê-la para sabermos qual é a quantidade total de brindes:
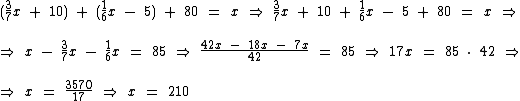
Logo:
a é a alternativa correta.
Resolução da Oitava Questão:
Percebemos claramente no enunciado que a dúzia do refrigerante custa R$ 30,00, pois comprando uma dúzia a menos, o preço passa de R$ 258,00 para R$ 228,00:
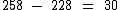
Três dúzias de refrigerante custam então R$ 90,00.
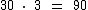
Descontando-se este valor dos R$ 258,00, obteremos o valor pago pelas 4 dúzias de suco:
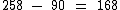
Que dividido por 4 nos dará o valor da dúzia do suco:
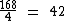
Para obtermos o valor unitário do suco, basta dividirmos este valor por 12:
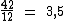
Portanto:
c é a alternativa correta.
Resolução da Nona Questão:
Partindo das informações disponíveis, vamos a busca das informações desejadas.
Se os meninos tivessem permanecido, os docinhos seriam repartidos igualmente entre as crianças, então cada uma delas iria receber exatamente 6 docinhos:
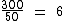
No entanto com a saída dos meninos, cada uma das meninas ganhou 9 docinhos a mais que os 6 aos quais tinha direito:
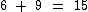
Ora, se cada uma delas recebeu igualmente 15 docinhos, então o número de meninas era:
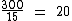
Como originalmente eram 50 crianças, então o número de meninos é igual a:
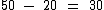
Assim sendo:
e é a alternativa correta.
Resolução da Décima Questão:
Para ficar mais fácil de expressarmos o nosso raciocínio, vamos chamar de x o número de saquinhos de 50 gramas. Em função disto podemos escrever a seguinte equação:
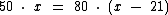
Ou seja, x saquinhos de 50 gramas equivalem a 21 saquinhos a menos de 80 gramas.
Resolvendo esta equação encontraremos a quantidade de saquinhos de 50 gramas:
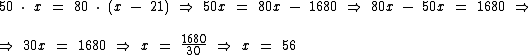
Pois bem, se temos 56 saquinhos de 50 gramas, então a quantidade torrada de amendoim foi de:
Observe que esta será a mesma quantidade se tivermos 21 saquinhos a menos de 80 gramas:
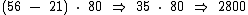
Logo:
d é a alternativa correta.
